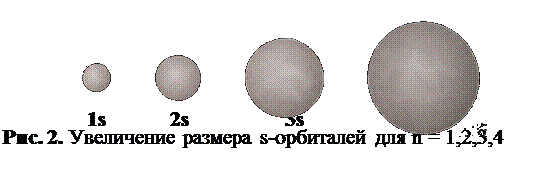Что показывает магнитное квантовое число
Магнитное квантовое число
Магни́тное ква́нтовое число́ — параметр, который вводится при решении уравнения Шрёдингера для электрона в водородоподобном атоме (и вообще для любого движения заряженной частицы).
Магнитное квантовое число (m) характеризует ориентацию в пространстве орбитального момента количества движения электрона или пространственное расположение атомной орбитали. Каждое из 2l+1 возможных значений магнитного квантового числа определяет проекцию вектора орбитального момента на данное направление (обычно ось z). Проекция орбитального момента импульса на ось z равна 
Иногда магнитное квантовое число определяют для проекции любого момента частицы (орбитального L, спинового S, суммарного J=L+S). В этом случае оно принимает соответственно 2L+1, 2S+1, 2J+1 значений. Для проекций спинового и суммарного моментов магнитное квантовое число может быть полуцелым.
Магнитное квантовое число в переходах между уровнями может изменяться лишь на определенное значение, устанавливаемое правилами отбора для данного типа перехода.
Что показывает магнитное квантовое число
Орбитальное квантовое число `l` показывает, сколько энергетических подуровней составляют данный уровень и характеризует форму орбиталей. Принимает значения от `0` до `(n-1)`.
При `n=3`, `l` принимает уже три значения: `0` `(s)`; `1` `(p)` и `2` `(d)`. Таким образом, на третьем уровне три подуровня. Орбитали `d`-подуровня имеют форму двух перекрещённых объёмных восьмёрок либо объёмной восьмерки с перемычкой (рис. 1).
При `n=4`, значений `l` уже четыре, следовательно, и подуровней на четвёртом уровне четыре. К перечисленным выше добавляется `3` `(f)`. Орбитали `f`-подуровня имеют более сложную, объёмную, форму.
Магнитное квантовое число `ml` определяет число орбиталей на каждом подуровне и характеризует их взаимное расположение.
Принимает значения `-l` до `+l`, включая `0`.
При `l=1`, `m_l` принимает три значения: `−1`; `0`; `+1`. Значит, орбиталей на данном подуровне (`p`-подуровне) три. Так как `p`-орбитали представляют из себя объёмные восьмёрки (то есть линейной структуры), располагаются они в пространстве по осям координат, перпендикулярно друг другу (`p_x`, `p_y`, `p_z`).
При `l=2`, `m_l` принимает уже пять значений: `−2`; `−1`; `0`; `+1`; `+2`. То есть на `d`-подуровне располагаются пять орбиталей. Это плоскостные структуры, в пространстве занимают пять положений.
Спиновое квантовое число `m_s` характеризует собственный момент количества движения электрона и принимает только два значения: `+1//2` и `-1//2`.
Всё вышесказанное можно обобщить в Таблице 2.
Таблица 2. Квантовые числа, атомные орбитали и число электронов на подуровнях (для `n
Квантовые числа (электронные оболочки)
Квантовые числа это числовое значение квантовой переменной определенного объекта (пример: электронная частица, ядра, атомы), которое характеризует его.
Квантовое число (полностью) характеризует состояние этой частицы.
Согласно современным взглядам стационарные состояния атома или термы характеризуются четырьмя квантовыми числами:
Что такое квантовые числа
При развитии теории Бора оказалось, что для полной характеристики стационарных состояний атома должно учитываться наличие у электронов не только круговых, но и эллиптических орбит (Зоммерфельд), а также и некоторые другие условия, которые увеличивают количество дозволенных энергетических уровней.
Главное квантовое число п определяет дозволенные энергетические уровни атома или в соответствии с моделью Резерфорда—Бора порядковые номера орбит и их радиусы (для эллиптических орбит — большую полуось).
Главное квантовое число может принимать значение любого числа натурального ряда:
Орбитальное или побочное квантовое число l определяет дозволенные значения момента количества движения lэ электрона по орбите.
В модели Бора—Зоммерфельда — дозволенные соотношения малой b и большой а полуосей эллиптических орбит (рис. , а):
где п — главное квантовое число.
Орбитальное квантовое число
Для основной орбиты атома водорода (квантовые числа атома водорода) п = 1 и l = (п — 1) = 0; b/a = 1/n = 1; эта орбита — круговая.
Если п > 1, то орбита имеет форму круга при l = (п — 1). Для примера на рис. , б показана группа орбит с главным квантовым числом n = 3 при трех значениях орбитального квантового числа:
Магнитное квантовое число
Магнитное квантовое число т1 определяет пространственную ориентировку электронных орбит, которая должна удовлетворять дозволенный значениям проекции орбитального момента, на некоторое направление.
В качестве такого направления рассматривается направление внешнего (действующего на атом) магнитного поля.
Движущийся вокруг ядра электрон образует элементарный круговой ток, имеющий собственное магнитное поле.
В результате взаимодействия внешнего магнитного поля с этим полем плоскость орбиты электрона ориентируется в пространстве определенным образом.
Дозволенными являются те положения орбиты, при которых численное значение l‘ э проекции вектора l Э момента количества движения электрона на направление магнитного поля (рис, справа) кратно величине h/2π : l ‘ э = ml (h/2 π), где ml — магнитное квантовое число.
Пример магнитного квантового числа
Для примера на рис. (справа) показано расположение орбиты электрона с некоторыми заданными главным и орбитальным квантовыми числами п и l и различным магнитным квантовым числом, которое изменяется в пределах тl = +1; тl = + 2 и тl — +3 (при отрицательных значениях этих чисел плоскости орбит поворачиваются на 180°).
Таким образом, при данных главном п и орбитальном l квантовых числах электрон в атоме, находящемся под действием магнитного поля, может двигаться по орбитам, имеющим в пространстве (2l + 1) различных положений. Этим положениям соответствуют свои энергетические уровни и, следовательно, линии в спектре (расщепление спектральных линий в магнитном поле называется явлением Зеемана).
Спиновое квантовое число

Тело, вращающееся вокруг своей оси (как, например, волчок), имеет собственный момент количества движения или момент вращения, с которым связаны особые механические свойства тела.
Такие же свойства имеет электрон (и другие элементарные частицы), хотя понятие о вращении вокруг своей оси к ним не применимо, вследствие отсутствия у них определенной внутренней структуры.
Поэтому электрону так же приписывается собственный момент количества движения, который называется спином.
Отсюда следует, что спиновое квантовое число электрона имеет только два значения:
Эти значения обусловливают две дозволенные ориентировки проекции S’ вектора спина S электрона на направление орбитального момента l: параллельную ms= +1/2 (рис. 2, а) и антипараллельную ms = — 1/2 (рис. 2, б).
Квантовые числа сохраняют свое значение и в атомах с большим числом электронов, хотя общая система обозначения состояний (термов) атома при этом усложняется.
Электронные оболочки
Группировка энергетических уровней атома (или орбит электронов по Боровской модели) происходит в соответствии со значением главного и побочного квантовых чисел.
Электроны с одинаковым главным числом п образуют электронные оболочки, которые принято обозначать следующими буквами:
n=1 2 34567.
К L М N О Р Q
Электроны, принадлежащие к определенной оболочке, образуют несколько подоболочек в соответствии с их орбитальным квантовым числом l. Значение этого числа и соответствующих ему подоболочек часто обозначают следующими буквами (буквы заимствованы из названий спектральных линий):
l = 0 1 2 3 4 5
s р d f g h
Поскольку орбитальное квантовое число принимает значения от 0 до (п — 1), число подоболочек равняется порядковому номеру п оболочки. Оболочка К состоит из одной подоболочки s: Оболочка L состоит из двух подоболочек s и р, оболочка М — из трех: s, р,d, и т. д.
Количество электронов в подоболочке обусловливается магнитным и спиновым квантовыми числами.
При этом выполняется принцип Паули: в атоме не может быть двух электронов, находящихся в тождественных состояниях движения, другими словами, не может быть больше одного электрона с четырьмя одинаковыми квантовыми числами.
Поскольку при заданном орбитальном числе l магнитное число тl может иметь (2l + 1) значений и при каждом из них спиновое число ms может иметь два значения, отличающихся знаком, общее количество возможных состояний при этом будет 2•(2l + 1).
Следовательно, подоболочка s (l = 0) может содержать только два электрона, различающиеся знаком спина; подоболочка р (l = 1) — шесть электронов, различающихся тремя магнитными числами и при каждом из них двумя спиновыми; подоболочка d (l = 2) — десять, и т. д.
Число электронов в подоболочке указывается как показатель степени у буквы, ее обозначающей.
Электронная оболочка пример

У гелия на этой же оболочке находится два электрона, отличающиеся спиновыми числами:
1s 2
(рис. 3, а, на котором слева показано схематическое, а справа — условное изображение оболочек).
У элементов второго периода таблицы Менделеева появляется вторая оболочка L. Она может состоять из двух подоболочек s и р.
Сначала запол няется подоболочка 2s (эллиптическая орбита): у лития одним электроном 1s 2 2s, у бериллия — двумя (с разными спиновыми числами) ls 2 2s 2 (рис. 3, б).
Затем заполняется подоболочка 2р (круговые орбиты) электронами с разными значениями магнитного квантового числа: у бора и углерода с ml = 0, у азота и кислорода с ml = + 1, у фтора и неона с тl = —1 (см. таблицу).
Таким образом, у неона подоболочка 2р заполнена шестью электронами:
ls 2 2s 2 2p 6
У натрия появляется третья оболочка М с одним электроном 1s 2 2s 2 2p 6 3s (рис. 3, г), и т. д.
Последовательность заполнения электронных оболочек сохраняется только у атомов первых 18 элементов.
Затем этот порядок усложняется: в одних случаях новый слой может начинать заполняться раньше, чем окончится заполнение предыдущего, в других случаях, наоборот, происходит заполнение оставшихся мест в предыдущей оболочке при неизменном числе электронов в наружном слое.
Количество электронов в наружной оболочке во всех случаях изменяется только от 1 до 8.
Наибольшее возможное число N электронов в оболочке соответствует условию:
N = 2п 2 ,
где п — главное квантовое число (для оболочки К —2, для L — 8, М — 18).
Это условие выполняется только для первых че тырех оболочек (К — N), для остальных — полное число электронов не достигает максимально возможного.
Сопоставление модели строения электронной оболочки атомов отдельных элементов с расположением их в периодической системе Д. И. Менделеева показывает, что периодичность повторения свойств элементов связана со сходством строения их электронных оболочек.
Число электронных оболочек соответствует номеру периода таблицы, к которому данный элемент принадлежит. В каждом периоде физико-химические свойства элементов связаны с числом электронов во внешнем слое, поэтому при образовании каждого нового слоя они повторяются.
Таким образом установленная Менделеевым периодичность свойств элементов получила новое обоснование в строении электронных оболочек атомов.
Спектр электромагнитного излучения
В связи с тем что радиусы электронных оболочек у атомов различных элементов обратно пропорциональны их порядковому номеру, у элементов с высоким номером орбиты электронов расположены значительно ближе к ядру.
Поэтому разность энергий между соседними уровнями, на которых находятся внутренние электроны, значительно выше, чем для внешних электронов, и для перевода их с одной орбиты на другую, особенно у атомов с высоким порядковым номером, требуется энергия, измеряемая сотнями и тысячами электрон-вольт.
Излучение, которое получается при этом, имеет значительно более высокую частоту и относится уже к дальнему ультрафиолетовому и рентгеновскому.
Имеется еще один механизм электромагнитного излучения — это торможение быстро движущихся электронов электрическим полем атома, внутри которого они пролетают. Фотоны излучения при этом имеют высокую энергию и относятся преимущественно к рентгеновскому излучению.
Еще большую энергию фотонов, чем рентгеновское излучение, и, следовательно, меньшую длину волны имеет гамма-излучение радиоактивных веществ, источником которого является атомное ядро.
Виды оптического излучения
В таблице приведены некоторые данные (частота, длина волны, энергия фотонов), характеризующие различные виды оптического излучения, рентгеновского и гамма-излучения.
| Элемент | Квантовые числа | Обозначение | |||
| п | l | тl | тs | ||
| Н | К (l = 0) | 0 | + 1/2 | 1s | |
| Не | -1/2 | 1s 2 | |||
| Li | L (l = 0) | 0 | + 1/2 | 1s 2 2s | |
| Be | -1/2 | 1s 2 2s 2 | |||
| В | р (l = 1) | 0 | + 1/2 | ls 2 2s 2 2p | |
| С | -1/2 | 1s 2 2s 2 2p 2 | |||
| N | +1 | + 1/2 | 1s 2 2s 2 2p 3 | ||
| О | -1/2 | 1s 2 2s 2 2p 4 | |||
| F | —1 | + 1/2 | 1s 2 2s 2 2p 5 | ||
| Ne | -1/2 | ls 2 2s 2 2p 6 | |||
| Вид излучения | Длина волны | Частота в гц | Энергия фотона в ЭВ | |||
| от | до | от | до | от | до | |
| Инфракрасное | 400 мк | 0,76 мк | 7,5•10 11 | 3,94• 10 14 | 0,0031 | 1,65 |
| Видимое | 760 ммк | 380 ммк | 3,94• 10 14 | 7,9• 10 14 | 1,65 | 3,3 |
| Ультрафиолетовое | 380 ммк | 10 ммк | 7,9• 10 14 | 3,0• 10 16 | 3,3 | 124 |
| Рентгеновское | 10 ммк | 0,001 ммк | 3,0•10 16 | 3,0•10 20 | 124 | 1,2•10 6 |
| Гамма | 0,1 ммк | не определен | 3,0•10 18 | 1,2•10 4 | ||
На рис. 3 приведен общий спектр электромагнитных волн, расположенных в порядке убывания длины волны. Разделение спектра на отдельные участки имеет условный характер, поэтому во многих случаях отдельные виды излучения перекрывают границы участков.
Статья на тему Квантовые числа
Похожие страницы:
Понравилась статья поделись ей
Состояние электронов в атоме
Состояние электронов в атоме описывается с помощью четырёх квантовых чисел: главного, орбитального, магнитного и спинового.
Главное квантовое число обозначается буквой n. Оно характеризует общий запас энергии электрона и выражается целыми числами натурального ряда: 1,2,3,4 и т.д. Электроны вокруг ядра образуют слои. Они называются квантовыми слоями или энергетическими уровнями и имеют буквенные обозначения: K,L,M,N и т.д. Номер слоя, в котором находится электрон, равен его главному квантовому числу. Если для какого-то электрона главное квантовое число равно 1, то он находится в первом (самом близком к ядру) энергетическом слое (K) и обладает минимальным запасом энергии. Если n = 2, электрон находится во втором квантовом слое (L) и т.д. Энергетический уровень объединяет все электроны с одинаковым значением главного квантового числа.
Количество квантовых слоёв в атоме определённого элемента зависит от его положения в периодической системе Д.И.Менделеева. Оно равно номеру периода, в котором находится данный элемент. Химические свойства атома зависят от строения его внешнего (самого удалённого от ядра) квантового слоя, номер которого также совпадает с номером периода. Для конкретного энергетического уровня существуют подуровни, определяемые орбитальным квантовым числом. Орбитальное квантовое число обозначается буквой l. Оно имеет столько значений, какова величина числа «n». Если n =1, то l имеет только одно значение; если n = 2, оно имеет два значения и т.д. Орбитальное квантовое число зависит от главного и принимает значения от 0 до (n–1). Каждому значению l соответствует свой подуровень в данном квантовом слое:n = 1 l = 0; один подуровень;n = 2 l = 0, 1; два подуровня;n = 3 l = 0, 1, 2; три подуровня;n = 4 l = 0, 1, 2, 3; четыре подуровня.Формально (математически) орбитальное квантовое число показывает количество узловых поверхностей, которые проходят через центральную точку атома — ядро. Под узловой поверхностью понимают плоскость, в которой электронная плотность равна нулю. Геометрически орбитальное квантовое число определяет форму электронной орбитали.Если l = 0, через ядро не проходит ни одной узловой поверхности. В этом случае электронная орбиталь обладает сферической симметрией. Она называется s-орбиталью и имеет форму шара (рис. 1).

Значение l = 1 показывает, что орбиталь имеет одну узловую поверхность, т.е. через ядро проходит одна плоскость, в которой электрон находиться не может. Тогда орбиталь принимает форму объёмной восьмёрки (или гантелеобразную форму) и называется p-орбиталью (рис. 3).
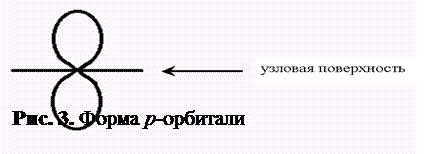 |
Если p-орбиталь принадлежит второму квантовому слою (n = 2), она обозначается 2p; если она находится в третьем квантовом слое, — 3p и т.д.
Магнитное квантовое число обозначается ml или просто mи принимает все значения от –l до +l. Оно характеризует положение орбитали в пространстве и показывает количество одноимённых орбиталей в данном квантовом слое.