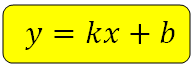Что показывает угловой коэффициент

Угловой коэффициент

Смотреть что такое «Угловой коэффициент» в других словарях:

угловой коэффициент — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN angle factor … Справочник технического переводчика

Угловой коэффициент прямой — Угловой коэффициент прямой коэффициент в уравнении прямой на координатной плоскости, численно равен тангенсу угла (составляющего наименьший поворот от оси Ox к оси Оу) между положительным направлением оси абсцисс и данной прямой линией.[1]… … Википедия

угловой коэффициент (прямой) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN slope … Справочник технического переводчика

угловой коэффициент кривой приёмистости бензина к тетраэтилсвинцу — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN lead susceptibility slope … Справочник технического переводчика

угловой коэффициент излучения — [angular coefficient of radiation] геометрическая xapактеристика взаимного расположения тел при лучистом теплообмене, определяемая телесным углом, в пределах которого 1 я поверхность излучает теплоту на 2 ю; Смотри также: Коэффициент… … Энциклопедический словарь по металлургии

локальный угловой коэффициент излучения — локальный угловой коэффициент излучения; локальный угловой коэффициент Отношение потока излучения от элементарной площадки одного тела на конечную поверхность другого тела к потоку собственного излучения, выходящему с элементарной площадки… … Политехнический терминологический толковый словарь

локальный угловой коэффициент — излучения; локальный угловой коэффициент Отношение потока излучения от элементарной площадки одного тела на конечную поверхность другого тела к потоку собственного излучения, выходящему с элементарной площадки первого тела по всевозможным… … Политехнический терминологический толковый словарь

средний угловой коэффициент излучения — средний угловой коэффициент излучения; средний угловой коэффициент Отношение потока излучения от поверхности одного тела на поверхность другого тела к полному потоку собственного излучения, выходящему со всей поверхности первого тела по… … Политехнический терминологический толковый словарь

средний угловой коэффициент — излучения; средний угловой коэффициент Отношение потока излучения от поверхности одного тела на поверхность другого тела к полному потоку собственного излучения, выходящему со всей поверхности первого тела по всевозможным направлениям в пределах… … Политехнический терминологический толковый словарь

элементарный угловой коэффициент излучения — элементарный угловой коэффициент излучения; элементарный угловой коэффициент Отношение потока излучения от элементарной площадки одного тела на элементарную площадку другого тела к потоку собственного излучения, выходящему с элементарной площадки … Политехнический терминологический толковый словарь

Источник

Линейная функция ее свойства и график. Угловой коэффициент линейной функции

Линейная функция

Линейная функция – это функция вида:

здесь k и b являются действительными числами.

Свойства линейной функции

Линейная функция имеет следующие свойства:

Угловой коэффициент линейной функции

Коэффициент k в формуле линейной функции называется угловым коэффициентом.

Угловой коэффициент определяет угол между графиком линейной функции и положительным направлением оси абсцисс.

График линейной функции

График линейной функции есть прямая. Вот график линейной функции y = 2x + 1

здесь угловой коэффициент больше нуля, угол прямой линии y = 2x + 1 с положительным направлением оси x – острый.

Как изменяется график линейной функции в зависимости от числа b в формуле линейной функции y = kx + b? Если b увеличивать, график смещается вверх, если число b уменьшать, то график y = kx + b смещается вниз.

График линейной функции y = kx + b построить вы можете сами прямо сейчас с помощью построителя графиков. Выберете в нём вид функции «Линейная: y = k * x + b» и нажмите кнопку «Построить график». Проведите эксперименты: устанавливайте угловые коэффициенты больше и меньше нуля, меняйте значения числа b и посмотрите, как будет изменяться график линейной функции.

Источник

Линейная функция

Линейная функция — функция вида График линейной функции — прямая.

Для построения графика линейной функции достаточно двух точек — потому что через две несовпадающие точки всегда можно провести прямую, причем единственную.

Угловой коэффициент прямой

Величина k в формуле линейной функции называется угловым коэффициентом прямой

Угловой коэффициент k равен тангенсу угла наклона графика линейной функции к положительному направлению оси Х.

Пусть Чем больше k, тем круче вверх идет график функции.

Заметим, что прямая (также изображенная на рисунке) не является графиком функции в нашем обычном, школьном смысле слова. В самом деле — мы помним, что функция — это соответствие между двумя множествами, причем каждому элементу множества Х соответствует один и только один элемент множества Y.

Для прямой это не выполняется: значению соответствует бесконечно много значений у.

Если прямые параллельны.

При этом, чем больше b, тем выше расположен на координатной плоскости график функции.

Например, прямые и параллельны. Их угловые коэффициенты равны.

Если прямые перпендикулярны. Например, прямые и пересекаются под прямым углом. Произведение их угловых коэффициентов равно — 1.

Построение графика линейной функции

График линейной функции построить легко — достаточно двух точек.

Оказывается, что привычный нам вид уравнения прямой — не единственно возможный.

Уравнение прямой можно записать также в виде

Построим, например, прямую, заданную уравнением

Значит, наша прямая проходит через точки и

Зачем изучать линейную функцию?

Дело в том, что многие зависимости в природе и технике описываются формулой виде

Например, закон Ома для участка цепи: Напряжение U прямо пропорционально силе тока I.

Обратите внимание, что в формулу линейной функции аргумент х входит в первой степени. Мы просто умножаем х на угловой коэффициент k и прибавляем b.

Источник

Угловой коэффициент прямой (и не только)!

Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:

— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.

Что такое абсцисса и ордината точки было описано в прошлой статье данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.

Уравнение прямой на координатной плоскости имеет вид:

где k – это и есть угловой коэффициент прямой.

Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох.

Он лежит в пределах от 0 до 180 градусов.

То есть, если мы приведём уравнение прямой к виду y = kx + b, то далее всегда сможем определить коэффициент k (угловой коэффициент).

Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.

Следующий теоретический момент! Уравнение прямой походящей через две данные точки. Формула имеет вид:

Рассмотрим задачи (аналогичные задачам из открытого банка заданий):

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).

В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:

Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:

*Оба катета равны шести (это их длины).

Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.

Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).

Формула уравнения прямой походящей через две данные точки имеет вид:

Наши точки имеют координаты (5;0) и (0;5). Значит,

Получили, что угловой коэффициент k = – 1.

Прямая a проходит через точки с координатами (0;6) и (8;0). Прямая b проходит через точку с координатами (0;10) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.

В данной задаче можно найти уравнение прямой a, определить угловой коэффициент для неё. У прямой b угловой коэффициент будет такой же, так как они параллельны. Далее можно найти уравнение прямой b. А затем, подставив в него значение y = 0, найти абсциссу. НО!

В данном случае, проще использовать свойство подобия треугольников.

Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.

Искомая абсцисса равна 40/3.

Прямая a проходит через точки с координатами (0;8) и (–12;0). Прямая b проходит через точку с координатами (0; –12) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.

Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.

Нам известны точки, через которые проходит прямая а. Можем составить уравнение прямой. Формула уравнения прямой походящей через две данные точки имеет вид:

По условию точки имеют координаты (0;8) и (–12;0). Значит,

Получили, что угловой k = 2/3.

*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.

Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:

Найти величину b мы можем подставив абсциссу и ординату в уравнение:

Таким образом, прямая имеет вид:

Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).

Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).

Формула уравнения прямой походящей через две данные точки имеет вид:

Наши точки имеют координаты (0;0) и (10;24). Значит,

Угловые коэффициенты параллельных прямых равны. Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:

Значение b найдём подставив в это уравнение координаты точки В(10;12):

Получили уравнение прямой:

Чтобы найти ординату точки пересечения этой прямой с осью оу нужно подставить в найденное уравнение х = 0:

*Самый простой способ решения. При помощи параллельного переноса сдвигаем данную прямую вниз вдоль оси оу до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу в точке (0;–12).

Искомая ордината равна –12.

Найдите ординату точки пересечения прямой, заданной уравнением

Координата точки пересечения заданной прямой с осью оу имеет вид (0;у). Подставим в уравнение абсциссу х = 0, и найдём ординату:

Ордината точки пересечения прямой с осью оу равна 3.

Найдите ординату точки пересечения прямых, заданных уравнениями

Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:

В первом уравнении подставляем – х вместо у:

Ордината равна минус шести.

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).

Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).

Прямая a проходит через точки с координатами (0;4) и (6;0). Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Прямая a проходит через точки с координатами (0;4) и (–6;0). Прямая b проходит через точку с координатами (0; –6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку B (6;4) и параллельной прямой, проходящей через начало координат и точку A (6;8).

Найдите абсциссу точки пересечения прямой, заданной уравнением 2х + 2у = 6, с осью ох.

Найдите абсциссу точки пересечения прямых, заданных уравнениями 3х + 2у = 6 и у = х.

Конечно, некоторые задачи, которые мы рассмотрели можно было решить более рациональными способами. Но ставилась цель показать разные подходы к решению. Надеюсь, это удалось.

1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.

2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.

3. Помните о том, что угловые коэффициенты параллельных прямых равны.

4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.

5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.

6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике. Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:

>> Угол наклона прямой от 0 до 90 градусов

>> Угол наклона прямой от 90 до 180 градусов

В данных двух случаях, по свойству тангенса :

То есть, чтобы найти уголвой коэффициент прямой, необходимо вычислить тангенс бетта в полученном прямоугольном треугольнике и записать результат с отрицательным знаком.

В данной рубрике продолжим рассматривать задачи, не пропустите!

Источник

Угловой коэффициент прямой

Что такое угловой коэффициент прямой? Если представить прямую, проходящую через две точки в прямоугольной системе координат (ОX, OY), то тангенс угла, образованного осью ОX и прямой – угловой коэффициент заданной прямой.

Например, угловой коэффициент прямой (а), проходящей через точки А (X1, Y1) и В (X2, Y2) будет равняться тангенсу (tg) треугольника, гипотенузой которого будет прямая (а) или отрезок АВ.

Таким образом можно узнать угол наклона прямой (а) к оси абсцисс ОХ. Угол определяется между осью ОХ и прямой (а) в направлении против часовой стрелки. То есть, если коэффициент наклона больше нуля (k›0), то угол наклона тупой. Если коэффициент наклона меньше нуля (k‹0), то угол наклона острый. Если коэффициент (k) равен нулю, то прямая (а) расположена параллельно оси ОХ. Если коэффициент (k) не существует – определяется в бесконечность – значит, прямая (а) расположена в системе координат параллельно оси OY.

Рассчитать угловой коэффициент можно с помощью онлайн калькулятора. Стоит всего лишь подставить данные точек в системе координат, через которые проходит заданная прямая, и калькулятор рассчитает угловой коэффициент. Подставив значения в уравнение прямой с угловым коэффициентом, можно определить – принадлежит ли некая произвольно заданная точка в системе координат данной прямой.

Источник