Как выглядит угол 120 градусов
Объясняем ребенку на пальцах одной руки, сколько градусов в угле
Метки
Как хотя бы примерно определить, сколько градусов в угле, если под рукой нет ни транспортира, ни угольника? «Так Просто!» знает остроумный способ и просто не может не поделиться им с читателями.
Сколько градусов в угле
Общепринятой единицей измерения плоских углов является градус. Почему математики древности выбрали именно такую единицу и почему в окружности 360 градусов, а не, скажем, 1000, точно неизвестно.
Одна из гипотез усматривает тут связь с тем, что в году приблизительно 360 дней. Другая гласит, что шумеры выбрали число 360, основываясь на своей шестидесятеричной системе счисления.
Так или иначе, а углы присутствуют не только на страницах учебников, но и повсеместно окружают нас в реальной жизни. Прямой угол легко найти в очертаниях зданий, изгибах мебели и каждом печатном листе.
Без угла в 45 градусов ни один столяр не смастерит простейшую рамку. Угол в 60 градусов требуется для построения равносторонних треугольников. Угол 30 градусов используется редко, но помогает получить угол в 120 градусов, необходимый для построения правильного шестиугольника.
Измеряем угол без транспортира
При наличии транспортира всё просто. Размести его центр в вершине угла, а основание совмести с одной из сторон. Проследи за второй стороной угла. В том месте, где она пересечет дугу транспортира, и будет указана величина угла в градусах.
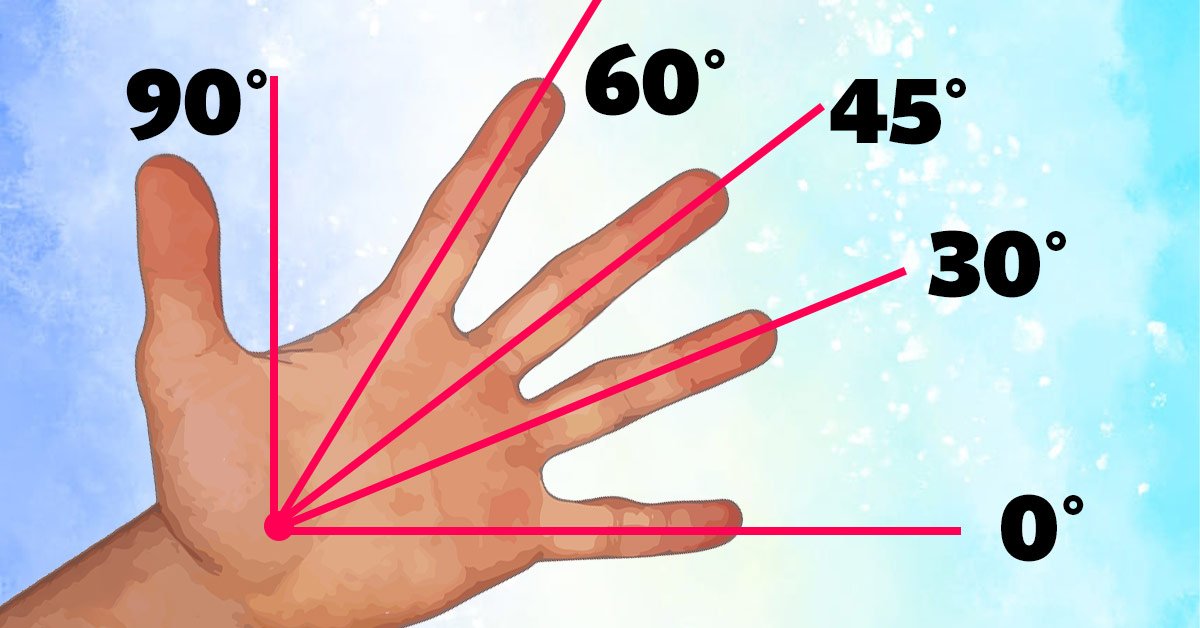
Без транспортира под рукой, как обычно и бывает, задача усложняется. Но смекалка выручит нас и здесь. Вытяни руку ладонью вверх и максимально расставь пальцы.
Следи за тем, чтобы большой палец находился перпендикулярно мизинцу. Тогда, если мизинец указывает на 0 градусов, то безымянный будет указывать на 30, средний на 45, указательный на 60, а большой на 90 градусов.
Строим углы в 90, 60 и 30 градусов без транспортира
Если нужен угол в 30, 60, 90 градусов, а транспортира или шаблона под рукой нет, помогут эти простые способы. Чтобы получить точный угол в 90 градусов, построй Пифагоров треугольник со сторонами, кратными 3,4,5.
Для этого, например, начерти отрезок длиной 5 см и проведи из его концов дуги с радиусами 3 и 4 см. Теперь соедини точку их пересечения с концами отрезка. Получится прямоугольный треугольник и угол, расположенный напротив гипотенузы, будет составлять ровно 90 градусов.
Когда уже есть прямой угол, легко получить углы в 30 и 60 градусов поможет магическое число 173 (его хорошо бы запомнить). Отложи по одной стороне прямого угла отрезок в 100 мм, а по другой — 173. Соедини их концы. Ты получишь шаблон с углами 90, 60 и 30 градусов!
Как выглядит угол 120 градусов
Добро пожаловать в сообщество «Котомафия»
Это сообщество о домашних кошках, в котором Вы можете делиться фото, историями и другим замурчательным контентом об аспектах жизни с мурчащими любителями тапок.
Котомафия- мимимишность и брутальность, мур=)
В сообществе категорически запрещено:
✔Оскорблять других пользователей. Запрещено использование нецензурных выражений и ругательств. Замена части букв значками «@», «#», «$» и т. д. при вычислимости исходного слова не избавляет от ответственности. Категорически не рекомендуется использование грубо-просторечной лексики, а также упоминания физиологических отклонений;
✔ Сообщения не по теме. Публикуемые сообщения должны соответствовать заявленной теме сообщества;
✔Размещение постов о помощи животным в сообществе без обязательных тегов: #вдобрыеруки #помощь #без рейтинга
Дорогие друзья, которым не нравятся посты с просьбами о помощи животным, очень просим Вас добавить теги: #помощь #вдобрыеруки и др. в черный список.
✔Плагиат! Не присваивай себе чужие идеи, записи и другой авторский контент.
✔Некорректные комментарии в комментариях, откровенный флуд, провокации, пропаганду жестокого и безответственного отношения к животным и пр. участники заносятся в черный список без дополнительных пояснений и предупреждений!
✔Нарушать правила Пикабу.
Не забывайте ставить тег «моё», «кот», «котомафия» если выкладываете своих любимцев.
Мы есть в Instagram: @kotomafia _fan, отмечайте нас на Ваших фото. Там уже есть интерактив и скоро конкурс с подарками/
Как с помощью циркуля и линейки построить угол, равный 120 градусов?
Следуя следующей схеме можно без труда построить угол 120°.
1) Используя линейку, рисуем прямую линию любой длины:
2) С помощью циркуля чертим дугу любого радиуса с центром в точке В, которая пересекает нашу линию в точке Q. (как показано ниже):
3) Теперь опять воспользуемся циркулем: тем же радиусом, но уже из точки Q рисуем еще одну дугу, которая пересекает первую дугу в точке R:
4) Снова берем циркуль с тем же радиусом чертим еще одну дугу, только в этот раз помещаем циркуль в точку R. Нам нужно пересечение двух дуг в точке P.
Постройте равносторонний треугольник. Для этого постройте любой отрезок и из каждой конечной точки проведите дугу радиусом, равным длине отрезка. Точку, где пересекутся дуги, соединяем с концами отрезка. Равносторонний треугольник готов. А внешний угол и окажется 120 градусов. Получится построение и с помощью линейки и с помощью циркуля.
Конечно же, ни через дефис, ни раздельно это слово не пишется. А пишется оно слитно: промокоды, промокод.
Так же пишутся и другие сложные слова, первой частью которых является промо*: промоакция, проморолик, промотреки, промоматериал, промодиджей, промоконсультант, промосайт, промокампания и др.
Слитное написание подобных слов соответствует существующему в русском языке орфографическому правилу, которое гласит, что сложные слова, образованные путём сложения части основы с целым словом, пишутся слитно, например: стенгазета, медсестра, замминистра, пединститут, видеоролик, метеосводка и пр.
Слово промокод, как и другие перечисленные мной слова с промо*, образовано именно так: от первого слова (промоутерский) взяли часть основы – промо* и сложили её с целыми словами – код, акция, ролик, материал и т.д.
Вот как на подобные вопросы отвечает справочная служба русского языка портала gramota.ru:
Справедливости ради замечу, что написание сложных слов с первой частью промо* установилось в русском языке не сразу, сначала эти слова писались и слитно, и раздельно, и через дефис – в общем, кто во что горазд, тот так и писал. Но любое иноязычное вкрапление в лексику русского языка рано или поздно начинает подчиняться правилам русского языка, что и произошло с данными словами: разнобой в их написании прекратился, так как нашлось правило, которое этот разнобой укротило и направило в единое русло.
Ещё замечу, что по другому правилу пишутся только сложные слова, образованные путём сложения части основы пол* (часть основы слова половина) с целым словом: среди таких слов есть и пишущиеся через дефис, и пишущиеся слитно, например: полстены, полкласса, но: пол-окна, пол-арбуза (второй корень начинается с гласной), пол-Москвы, пол-Смоленска (второй корень начинается с прописной буквы), пол-лимона, пол-литра (второй корень начинается с буквы Л, исключение – поллитровка), а когда между пол* и вторым корнем вклинивается прилагательное, то всё выражение пишется раздельно – в три слова: полдоски – пол классной доски, пол-ложки – пол чайной ложки.
Некоторые страны, заботясь о своем статусе в мировом сообществе, о развитии своих технологий, о достижении главенства среди других стран уделяют особое внимание подрастающему поколению, их образованию. Таким образом, они готовят себе достойную смену, способную и дальше развивать и поднимать престиж своей страны.
Увы, почему-то руководители нашей стран образованию подрастающего поколения уделяют совсем мало внимания. По всей видимости, в этом тоже скрыта какая-то цель.
То есть каждый целеустремлённый человек по своей сути является мечтателем. И при достижении своей цели он желает заполучить что-то новое, что-то близкое и одновременно неощутимое. Значит он строит новую цель, вырабатывает новые пути её достижения и постоянно не расстаётся с мыслью, что ещё чуть-чуть и он заполучит свой вожделенный объект. Этот круг повторяется бессчётное число раз, на протяжении всей жизни человека.
Это лично только мои мысли, можете выбрать отсюда что-нибудь или немного дополнить текст и переписать.
Аутизм – это существенное отклонение в психическом здоровье от нормы. Ребенок, страдающий аутизмом, с огромным трудом находит общий язык со своим окружением, в том числе даже с самыми близкими людьми – мамой и папой. Это очень сложно для него, поскольку эти процессы протекают в головном мозге – именно там расположен этот патологический процесс, мешающий ребенку включиться в обычную жизнь. Помимо психологических трудностей в общении, эти детки отличаются в большинстве случаев плохим развитием речи, нарушением моторики, низким уровнем обучаемости. Хотя есть примеры того, как при каждодневной упорной работе с такими детьми, любви к ним удается достичь приличных успехов. Дети начинают лучше говорить, проявлять какие-то эмоции, не избегают общения, овладевают определенными навыками.
Поэтому отношение у меня к данному «пилотному» проекту двойственное. С одной стороны, есть надежда, что, оказавшись в среде сверстников, страдающие аутизмом детки все-таки начнут потихоньку включаться в социальную жизнь. Может быть, это даст им возможность понять, что помимо их маленького мирка есть мир большой и разноцветный, разнообразный, что в нем много людей и что сам ребенок тоже принадлежит этому сообществу. Возможно, обычная школа, обычный класс и нормальные дети помогут ребенку с аутизмом лучше адаптироваться во внешней среде.
Другой стороны, я прекрасно знаю, какими жестокими бывают дети(. Если в их коллектив попадает новый человечек с какими-то отклонениями в здоровье, его могут задразнить (это самое мягкое издевательство) так, что он просто замкнется в себе и откажется ходить в школу. А ведь ребенку с аутизмом замыкаться дальше уже просто некуда! Дефект речи и моторики послужат лишним поводом для насмешек и издевательств со стороны других детей. Тут уж на учителя ложится огромная ответственность, чтобы не дать в обиду больного ребенка и воспитать чувство доброты и сочувствия в остальных учениках.
Так что, проблема эта очень сложная. Как бы не сделать хуже ребенку, ради которого все эти старания…
Таблица градусов и углов, с примерами решений
И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
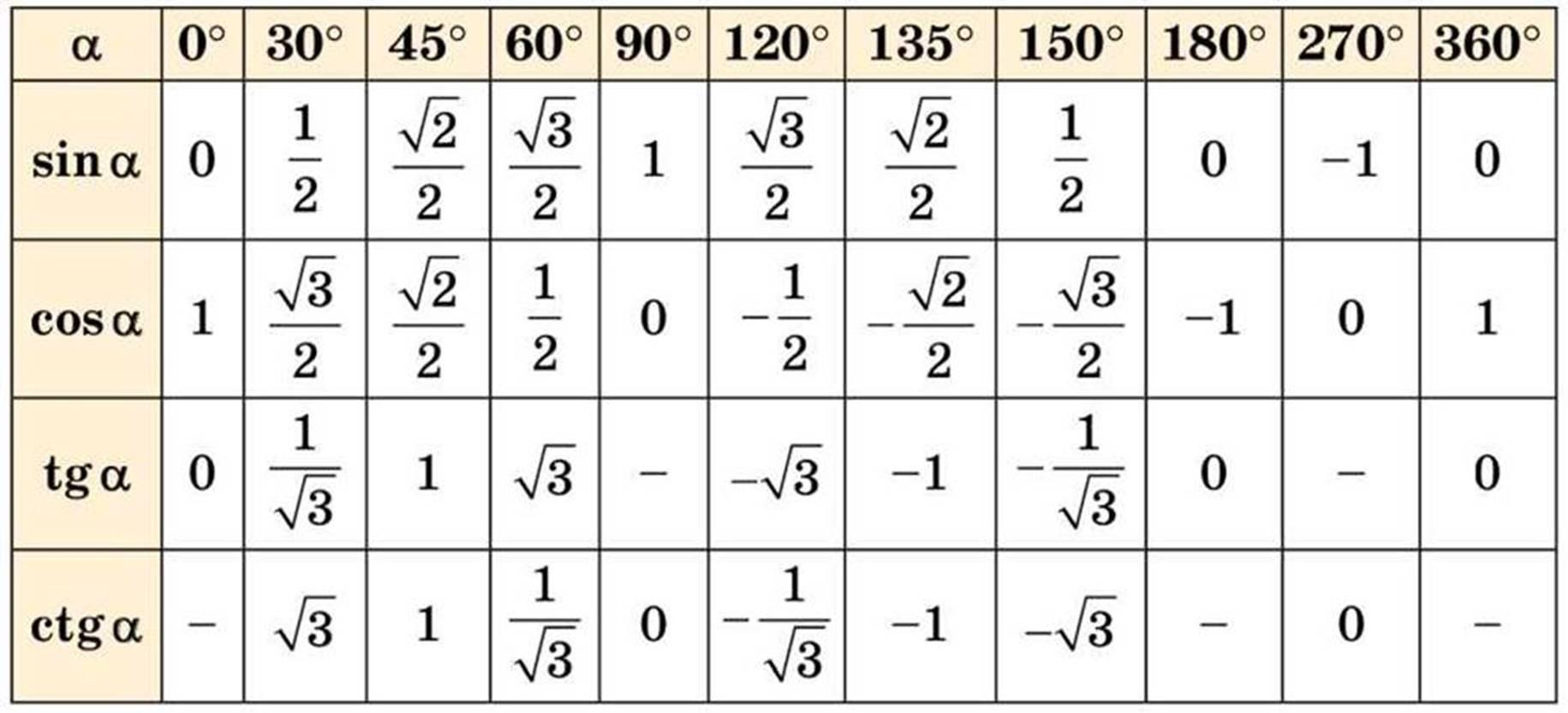
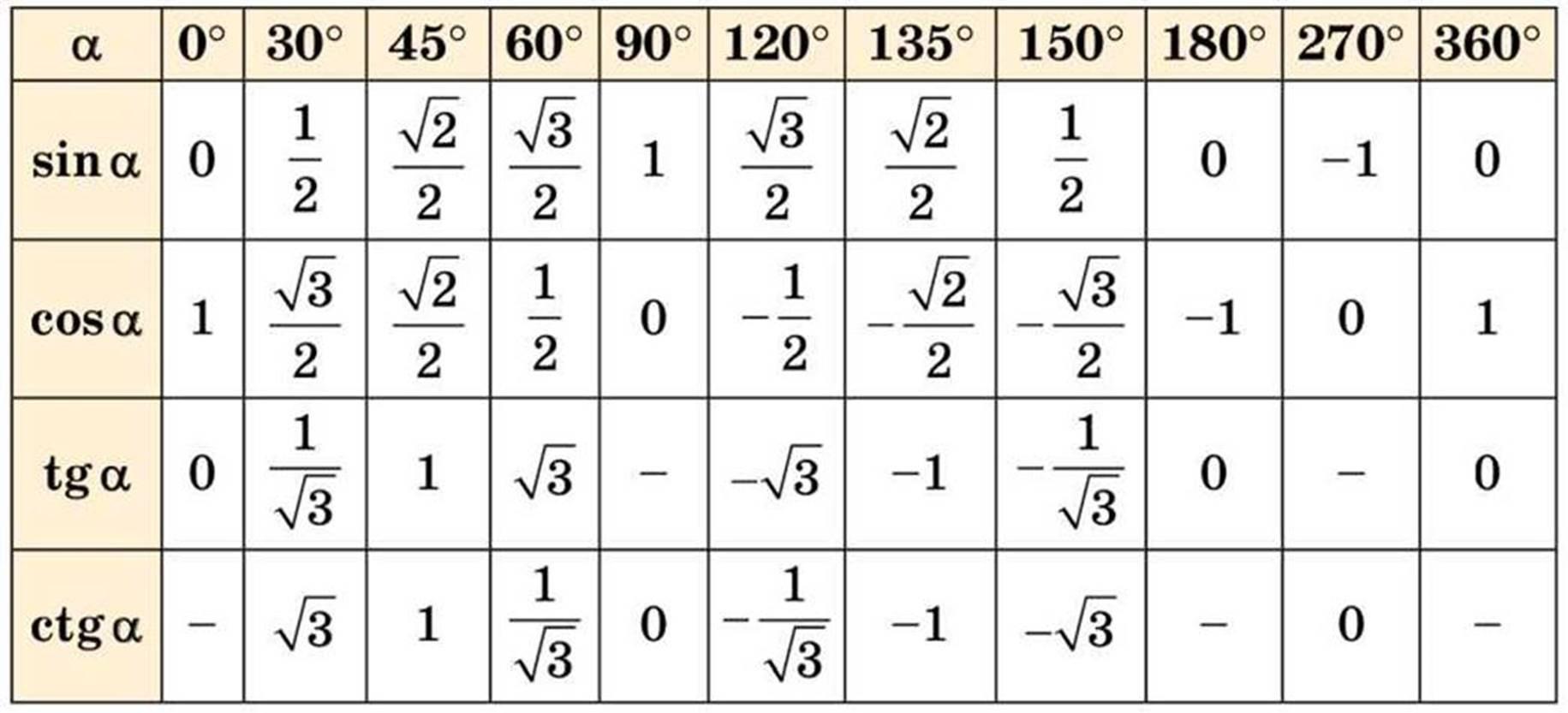
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90. градусов.
Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 00+3600*z …. 3300+3600*z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.

Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 200 = 0.9397
Значения tg угла до 900 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 780 37мин = 4,967
а ctg 200 13мин = 25,83
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в х!
Заметка: Стеновые отбойники — отбойная доска для защиты стен (http://www.spi-polymer.ru/otboyniki/)
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Измерение углов
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами.
Углы больше 360 градусов
Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.
Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.
Положительные и отрицательные углы
Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.

Угол равен 360 + 50 = 410°
Радиан

Радиус = r = OA = OB = AB
Радианная и градусная мера угла
Здесь рассматриваем задачи Proc32 — Proc33 из задачника Абрамяна: описание функций преобразования углов из градусов в радианы и наоборот.
Так что такое радианная мера угла? Рассмотрим некоторую окружность радиуса R с центром в точке О. Поскольку окружность делится на 360 градусов, а длина окружности равна 2πR, то на 1 градус приходится длина дуги равная 2πR/360 = πR/180. Тогда углу α градусов соответствует длина дуги L = πRα/180.
В этом смысле очень интересна ситуация, когда длина дуги L равна радиусу окружности R. Каков при этом угол дуги? Вспоминая предыдущую формулу для вычисления длины дуги, имеем: πRα/180 = R, откуда πα/180 = 1, а отсюда получаем α = 180/π.
Например, если длина дуги равна 1.5R, то радианная мера угла этой дуги равна 1.5; если длина дуги равна 0.25R, то радианная мера равна 0.25; для дуги длиной 2πR (вся окружность) радианная мера равна 2π и т.д. Вообще, для дуги длиной L угол в радианах равен L/R, где R – радиус.
Радиан – это очень удобный способ измерения углов, поскольку вместо самих углов мы можем оперировать коэффициентами отношений длин дуг и их радиусов. В высшей математике во всех тригонометрических функциях используется только радианная мера.
Proc32. Описать функцию DegToRad(D) вещественного типа, находящую величину угла в радианах, если дана его величина D в градусах (D — вещественное число, 0 ≤ D https://progmatem.ru/proc/proc-32-33.html
Радианная и градусная мера угла
В школьном курсе математики есть два определения основных тригонометрических функций — синуса, косинуса, тангенса и котангенса:
Для решения задачи B11 нужен именно алгебраический подход. Чуть позже мы убедимся, что такие задачи решаются элементарно — буквально с помощью одной формулы. Но для начала научимся быстро (буквально на лету) определять координатную четверть, в которой расположен искомый угол. В этом нам помогут следующие правила.
Переход от радианной меры к градусной
Вспомните: в 8—9 классах мы работали лишь с несколькими стандартными углами. А именно: 30°, 45° и 60°. В особо продвинутых случаях учителя рассказывали еще об углах 90° и 0°. Любые другие значения назывались «сложными», и возникновение таких углов, скорее всего, указывало на ошибку в решении.
С введением тригонометрической окружности все ограничения на углы отпадают. Здесь я не буду рассказывать, как устроена тригонометрическая окружность — все это подробно описано в любом учебнике по математике. Вместо этого предлагаю обсудить другой вопрос — более важный, но которому почему-то не уделяется достаточно внимания. Речь идет о переходе от радианной меры угла к градусной.
Исторически так сложилось (и небезосновательно), что углы на тригонометрической окружности измеряют в радианах. Например, полный оборот — 360° — обозначается как 2π радиан. А всеми любимый (или ненавидимый) угол 45° равен π/4 радиан.
У многих возникает вопрос: при чем здесь число π? Ведь π ≈ 3,14. Так вот, чтобы избежать путаницы, запомните простое, но очень важное правило:
Во всех тригонометрических функциях — синусе, косинусе, тангенсе и котангенсе — можно без ущерба для здоровья заменять число π на 180°. Пишется это так: π → 180°.
Обратите внимание: данное правило работает только для тригонометрических функций! Например, мы спокойно можем записать sin π = sin 180°. Но если мы хотим найти примерную длину отрезка l = 5π, придется считать: l = 5 · π ≈ 5 · 3,14 = 15,7.
Разумеется, существует и обратное правило — переход от градусной меры угла к радианной. Однако нас это сейчас не интересует, поскольку в задачах B11 такой переход не встречается.
Теперь взгляните на конкретные примеры:
Задача. Перейдите от радианной меры угла к градусной (значение тригонометрических функций вычислять не надо):
Итак, перед нами восемь тригонометрических функций, аргументы которых заданы в радианах. Мы можем перейти от радианной меры аргументов к градусной по правилу: π → 180°. Имеем:
Итак, вместо непонятного множителя π мы получаем вполне вменяемое число, которое можно умножать и делить по стандартным правилам.
Границы координатных четвертей
Теперь, когда мы умеем заменять радианную меру углов градусной, попробуем переписать всю тригонометрическую окружность. Это будет ключом к решению задачи B11.
Основные правила останутся прежними: «нулевой градус» совпадает с положительным направлением оси ОХ, а углы откладываются в направлении против часовой стрелки.
Но числа, стоящие на границах координатных четвертей, станут другими. Взгляните:
Отныне вместо непонятных «пи» и «пи-пополам» используйте простую и понятную шкалу:
Хорошая новость состоит в том, что эти правила очень быстро откладываются в голове — стоит лишь немного потренироваться. И вы точно не забудете эти числа на ЕГЭ по математике, чего нельзя сказать про радианную меру.
Если же память на числа плохая, могу посоветовать одну хитрость. Взгляните еще раз на границы координатных четвертей: 90°, 180°, 270° и 360°. Первая из них — 90° — это прямой угол, знакомый еще из курса средней школы. Его вы точно не забудете.
Остальные углы отличаются друг от друга на эти же самые 90°. Взгляните: 90° + 90° = 180°; 180° + 90° = 270°; 270° + 90° = 360°.
Таким образом, даже если вы забудете эти числа, их всегда можно восстановить, если просто запомнить, что прямой угол — это 90°.
А теперь разберем конкретные примеры. Будем учиться искать координатные четверти быстро, поскольку от этого умения напрямую зависит решение задачи B11.
Задача. Определите, в какой координатной четверти находится аргумент тригонометрической функции:
Для начала переведем все углы из радиан в градусы по правилу: π → 180°. А затем найдем координатную четверть, ориентируясь по границам: 90°, 180°, 270°, 360°. Имеем:
Как видите, далеко не всегда можно найти значение самой тригонометрической функции. Например, попробуйте вычислить cos 162° или sin 108°. Зато мы всегда можем определить, в какой координатной четверти находится данный угол.
Нестандартные углы и периодичность
До сих пор мы рассматривали углы α ∈ [0°; 360°].
Но что произойдет, если, например, угол α = 420°? А как насчет отрицательных углов? Такие углы редко встречаются на ЕГЭ по математике (по крайней мере, в части B), но лучше застраховать себя от подобных «неожиданностей», поэтому предлагаю разобрать и такие задачи. Тем более, схема решения практически ничем не отличается от «стандартных» углов.
Итак, что если угол α > 360°? Судя по тригонометрической окружности, точка сделает полный оборот — а затем пройдет еще чуть-чуть. Это самое «чуть-чуть» вычисляется очень просто. Достаточно отнять от исходного угла величину 360° (иногда это приходится делать несколько раз).
С отрицательными углами работаем аналогично. Если добавлять к отрицательному углу величину 360°, мы очень скоро получим новый угол α ∈ [0°; 360°]. Таким образом, вся схема решения выглядит следующим образом:
Задача. Определите, в какой координатной четверти находится аргумент тригонометрической функции:
Снова переводим все углы из радиан в градусы по правилу: π → 180°. Дальше уменьшаем или увеличиваем аргумент на 360° до тех пор, пока он не окажется на отрезке [0°; 360°]. И только затем выясняем координатную четверть. Получим: