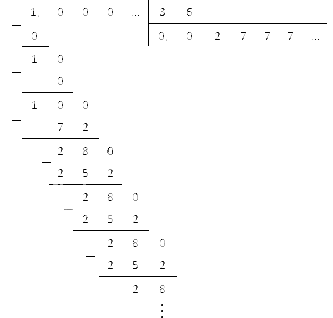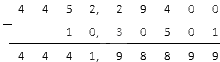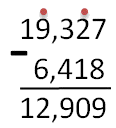Как выполняется вычитание десятичных дробей
Вычитание десятичных дробей
Также как и сложение, вычитание десятичных дробей производим по правилам вычитания в столбик натуральных чисел.
Основные правила вычитания десятичных дробей.
Как вычитать десятичные дроби другим способом
Если вы чувствуете себя уверенно в десятичных дробях и хорошо понимаете, что называется десятыми, сотыми и т.д., предлагаем вам попробовать другой способ вычитания (сложения) десятичных дробей без их записи в столбик.
Другой способ вычитания десятичных дробей, как и сложение, основывается на трёх основных правилах.
Вычитают десятичные дроби справа налево. То есть, начиная с самой правой цифры после запятой.
Вычитать нужно по цифрам разрядов. Целые из целых, десятые из десятых, сотые из сотых, тысячные из тысячных и т.д.
При вычитании большей цифры из меньшей, у соседа слева меньшей цифры занимаем десяток.
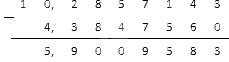
Как обычно, рассмотрим пример:
Вычитаем справа налево с самой правой цифры. У нас самая правая цифра в обеих дробях — сотые. 1 — в первом числе, 1 — во втором. Вот их и вычитаем.
И наконец, вычитаем целые части. 14 — в первом числе (не забудьте, что мы из 5 вычли 1 ), 8 — во втором числе.
Десятые можно вычитать только из десятых, сотые из сотых, тысячные из тысячных и т.д. Если в одной из десятичных дробей, отсутствует цифра нужного разряда, вместо неё пишем ноль.
Во втором числе самая правая цифра это 2 (сотые), а в первом числе сотых нет в явном виде. Поэтому, к первому числу справа от 9 добавляем ноль и вычитаем согласно основным правилам.
Вычитание десятичных дробей: правила, примеры
В данной публикации мы рассмотрим, каким образом из десятичной дроби можно вычесть другую дробь (десятичную и обыкновенную) или целое натуральное число (и наоборот). Также разберем примеры для лучшего понимания представленного материала.
Правило вычитания десятичных дробей
Разность десятичных дробей находится путем их вычитания столбиком. Алгоритм приведен ниже:
1. Располагаем дроби так, чтобы их запятые были строго друг под другом. Таким образом, друг под другом окажутся и одноименные разряды: десятые под десятыми, сотые под сотыми, тысячные под тысячными и т.д.
Примечание: Если число знаков после запятой у дробей разное, в конце дроби с меньшим количеством цифр в дробной части добавляем нули, чтобы уравнять ее по длине с другой. Согласно основному свойству десятичной дроби, это никак не повлияет на ее величину.
Примеры неправильной записи разности:
Примеры правильной записи разности:
2. Не обращая внимания на запятые вычитаем из одной дроби другую (т.е. условно принимаем их за целые числа).
3. В полученном результате добавляем запятую в том же месте, где расположены запятые дробей выше.
Разность десятичной дроби и целого натурального числа
Если требуется найти разность десятичной дроби и целого натурального числа, в конце последнего ставим запятую, после которой дописываем столько нулей, сколько знаков содержится после запятой в десятичной дроби. Далее выполняем требуемое действие, т.е. вычитание.
Разность десятичной и обыкновенной дробей
Чтобы найти разность десятичной и простой дробей, последнюю переводим в десятичную. Далее выполняем вычитание.
Альтернативный вариант – наоборот, десятичную дробь преобразовать в обыкновенную. Здесь мы уже будем вычитать простые дроби.
Примеры
Вычислим разности десятичных дробей, которые рассмотрели выше:
А теперь давайте посмотрим примеры вычитания из десятичной дроби целого натурального числа и наоборот.
Правила вычитания десятичных дробей в математике
Вычитание десятичных дробей в математике
Десятичная дробь — это вид дроби, является методом записи действительных чисел в таком виде:
, — десятичная запятая, отделяет целую часть от дробной части числа;
d k — десятичные цифры.
Последовательность чисел, которые стоят до запятой, является конечной. Последовательность чисел после запятой конечна или бесконечна.
Такое действительное число равно сумме конечного или бесконечного числа слагаемых.
Представлять действительные числа, как десятичные дроби, — значит, обобщать записи целых чисел в десятичной системе счисления. Когда целое число записывают в виде десятичной дроби, после запятой не будет других цифр, кроме нулей:
что соответствует записи данного числа в десятичной системе счисления.
Сложение и вычитание десятичных дробей выполняется путем записи их друг под другом, чтобы запятая была под запятой. Далее действия аналогичны операциям с обычными числами. В ответ нужно перенести запятую.
Как вычитать десятичные дроби в столбик
В процессе вычитания десятичных дробей, как и сложения, необходимо руководствоваться правилами, согласно которым вычитают в столбик натуральные числа. Последовательность действий:
Альтернативный способ
Существует другой способ вычитания десятичных дробей. При этом не требуется записывать их в столбик, а действия следует выполнять, опираясь на следующие правила:
Разобрать этот способ можно на примере:
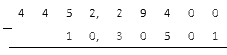
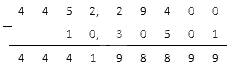
Проводим вычитание, двигаясь с правой стороны в левую. Самой правой цифрой в обеих дробях — сотые. 1 — в первом числе, 1 — во втором. Найдем их разность:
В результате получен 0, который следует записать на месте сотых в разности:
Далее следует из десятых вычесть десятые. 2 — в первом числе, 3 — во втором числе. Заметим, что из 2 (меньшего) нельзя отнять 3 (большее), поэтому нужно занять десяток у соседа с левой стороны для 2. В данном случае, это 5. Получается, что 3 вычитается из 12:
В десятые нового числа можно записать 9. Важно помнить о необходимости вычитания единицы из 5, так как был занят десяток из 5.
Переходим к вычитанию целых частей. 14 — в первом числе, 8 — во втором числе.
Десятые допускается вычитать лишь из десятых, сотые из сотых, тысячные из тысячных и так далее. Когда одна из десятичных дробей не имеет цифру необходимого разряда, ее можно заменить нулем.
Рассмотрим вычитание десятичных дробей:
Второе число в крайнем правом положении имеет 2 (сотые), а в первом числе сотые отсутствуют. В этом случае необходимо к первому числу с правой стороны от 9 дописать ноль и выполнить вычитание по стандартному алгоритму.
Вычитание десятичных дробей с разными знаками
Вычитать обычные дроби, имеющие неодинаковые знаки, следует по правилам:
Как вычесть десятичную дробь из смешанного числа или обыкновенной дроби и наоборот
Когда нужно вычислить разность десятичной дроби и целого натурального числа, в конце последнего необходимо дописать запятую, а после нее проставить нули в количестве, равном количеству знаков после запятой в десятичной дроби. Затем нужно выполнить вычитание.
Если необходимо найти разность десятичной дроби и простой дроби, то следует рассмотреть 2 варианта и выбрать наиболее подходящий:
В качестве примеров можно рассмотреть вычитание десятичных дробей:
Примеры вычитания числа, которое является целым и натуральным, из десятичной дроби, а также обратный случай:
Вычитание десятичной дроби из смешанной, или наоборот, выполняют путем приведения дроби к единому виду дробей.
Данное правило распространяется на все виды дробей при их вычитании и сложении. Рассмотреть действие можно на примере:
В первую очередь требуется проверка возможности перевода знаменателя смешанной дроби в число, кратное 10, 100 и так далее. Другими словами, необходимо какое-либо из перечисленных чисел разделить на знаменатель. В этом случае при умножении на знаменатель 5 числа 2 получается 10.
Далее следует отделить единицу, то есть целое, умножить дробь на 2. Умножение предусмотрено для числителя и знаменателя. Так как множитель одинаковый, то значение дроби не меняется:
После возврата единицы получим:
Вычитание смешанной дроби из десятичной выполняют путем перевода десятичной дроби в смешанную.
Рассмотрим действие на примере:
Отделим целые части от дробных:
Далее следует определить минимальный единый знаменатель. Это число 10. Умножим вторую дробь на 2:
Далее нужно вычесть дробные части:
Сложим целую и дробную часть, чтобы получить ответ:
Примеры решения задач для 5 класса
В данном случае количество цифр после запятой разное. Поэтому к 3,1 после единицы нужно дописать пару нулей: 3,100. Далее нужно записать выражение в столбик и выполнить вычисления:
Нужно найти разность:
Запишем выражение в столбик:
Начать следует с вычитания самостоятельных сотых частей: 6-9. При этом необходимо занять единицу у соседнего разряда:
Полученный ответ нужно записать на место сотой части:
Далее можно приступить к вычитанию десятых частей. Следует помнить, что ранее была занята единица. Таким образом, в десятых вместо 4 осталась цифра 3. Выполним вычисления в десятых:
Полученный результат нужно записать в десятые:
Затем можно вычесть целые части:
Единицу, которая получилась в результате, следует записать в целой части ответа:
Целую часть нужно отделить от дробной:
Требуется решить выражение:
Выражение необходимо записать в столбик:
Следует сравнять количество цифр после запятой путем постановки запятой после 3 и записи одного нуля:
Далее можно приступить к вычитанию десятых частей: 0 – 2. При этом необходимо занять единицу у соседнего разряда:
Затем требуется вычесть целые части с учетом того, что была занята единица, и отделить с помощью запятой дробную часть:
Требуется отделить целую часть от дробной и вычесть из нее указанное число:
Вычитание десятичных дробей: правила, примеры, решения
Изучаем другие действия, которые можно совершать с десятичными дробями. В этом материале мы узнаем, как правильно подсчитать разность десятичных дробей. Отдельно разберем правила для конечных и бесконечных дробей (как периодических, так и непериодических), а также посмотрим, как считать разность дробей столбиком. Во второй части мы объясним, как вычесть десятичную дробь из натурального числа, обыкновенной дроби, смешанного числа.
Отметим заранее, что в этой статье рассмотрены только случаи, когда меньшая дробь вычитается из большей, т.е. результат этого действия положителен; другие случаи относятся к нахождению разности рациональных и действительных чисел и должны быть объяснены отдельно.
Основные правила вычитания десятичных дробей
Процесс вычисления как конечных, так и бесконечных периодических десятичных дробей можно свести к нахождению разности дробей обыкновенных. Раньше мы говорили о том, что десятичные дроби можно записывать в виде обыкновенных дробей. Исходя из этого правила, разберем несколько примеров нахождения разности.
Решение
Подсчеты, связанные с десятичными дробями, удобно производить столбиком. Как же пользоваться этим методом? Покажем, решив задачу.
Решение
Переведем записи периодических дробей в обыкновенные и подсчитаем.
Если нужно, ответ мы можем представить в виде десятичной дроби:
Разберем далее, как найти разность, если у нас в условиях стоят бесконечные непериодические дроби. Такой случай также можно свести к нахождению разности конечных десятичных дробей, для чего понадобится округлить бесконечные дроби до определенного разряда (обычно самого меньшего из возможных).
Решение
Как считать разность десятичных дробей столбиком
Вычитание столбиком – быстрый и наглядный способ узнать разность конечных десятичных дробей. Процесс подсчета очень схож с аналогичным для натуральных чисел.
Чтобы подсчитать разность десятичных дробей столбиком, необходимо:
Разберем конкретный пример использования этого метода на практике.
Решение
Запишем получившиеся числа друг под другом в нужном порядке, чтобы получился столбик:
Считаем как обычно, игнорируя запятые:
В получившемся ответе поставим запятую в нужном месте:
Как вычесть натуральное число из десятичной дроби и наоборот
Найти разность между конечной десятичной дробью и натуральным числом легче всего описанным выше способом – столбиком. Для этого число, из которого мы вычитаем, необходимо записать в виде десятичной дроби, в дробной части которой стоят нули.
Если из натурального числа нам нужно вычесть бесконечную периодическую дробь, то мы опять же сводим эту задачу к аналогичному вычислению. Заменяем периодическую десятичную дробь на обыкновенную.
Решение
Если данная в условии дробь непериодическая, поступаем так же, предварительно округлив ее до нужного разряда.
Решение
Если перед нами стоит обратная задача – вычесть натуральное число из десятичной дроби, то мы выполняем вычитание из целой части дроби, а дробную часть не трогаем совсем. Мы поступаем так и с конечными, и с бесконечными дробями.
Решение
Как вычесть десятичную дробь из смешанного числа или обыкновенной дроби и наоборот
Эту задачу также необходимо свести к вычитанию обыкновенных дробей – как в случае со смешанными числами, так и с десятичными дробями.
Решение
Если в условии стоит смешанное число, из которого надо вычесть конечную или периодическую десятичную дробь, то поступаем аналогично.
Таким же образом мы действуем, когда вычитаем смешанное число или обыкновенную дробь из конечной или периодической дроби.
Решение
Если нам требуется выполнять вычитание с участием бесконечных непериодических дробей, то нам нужно будет свести их к конечным. Со смешанными числами поступаем аналогично. Для этого запишем обыкновенную дробь или смешанное число в виде десятичной дроби и округлим вычитаемую дробь до определенного разряда. Проиллюстрируем нашу мысль примером:
Решение
Преобразуем смешанное число в неправильную дробь.
10 2 7 = 10 · 7 + 2 7 = 72 7
Единственное, что осталось сделать – вычесть одну конечную десятичную дробь из другой. Выполним подсчет столбиком:
Дроби. Вычитание десятичных дробей.
Первый вариант вычитания десятичных дробей:
Основные правила вычитания десятичных дробей.
Второй вариант вычитания десятичных дробей:
Если вы хорошо разбираетесь в десятичных дробях, в том, что такое десятые, сотые и др., то вам будет интересен этот вариант.
Правила вычитания десятичных дробей в строчку:
Записываем 9 в разность. Так как мы из 5 вычли 1 десяток, в уменьшаемом остается не 15, а 14, чтобы это не забыть ставим над 5 пустой кружок или точку, как удобнее.
Во втором числе крайняя правая цифра это два (сотый разряд), а в первом числе сотых не видно. Значит, к первому числу справа от 9 дописываем 0 и далее производим вычитание опираясь на основные правила.
Третий вариант вычитания десятичных дробей: