Как выразить игрек в системе

02.01.202420.09.2023 admin 0 Comments

Урок «Системы уравнений»

Краткое описание документа:

Для изучения сегодняшней темы нам необходимо вспомнить, какие способы решения систем уравнений с двумя переменными нам известны.

Для решения систем уравнений с двумя переменными использовались такие способы, как метод подстановки, алгебраического сложения, введения новых переменных, графический метод.

Сегодня на уроке мы рассмотрим несколько необычные применения этих методов, другие способы решения систем уравнений.

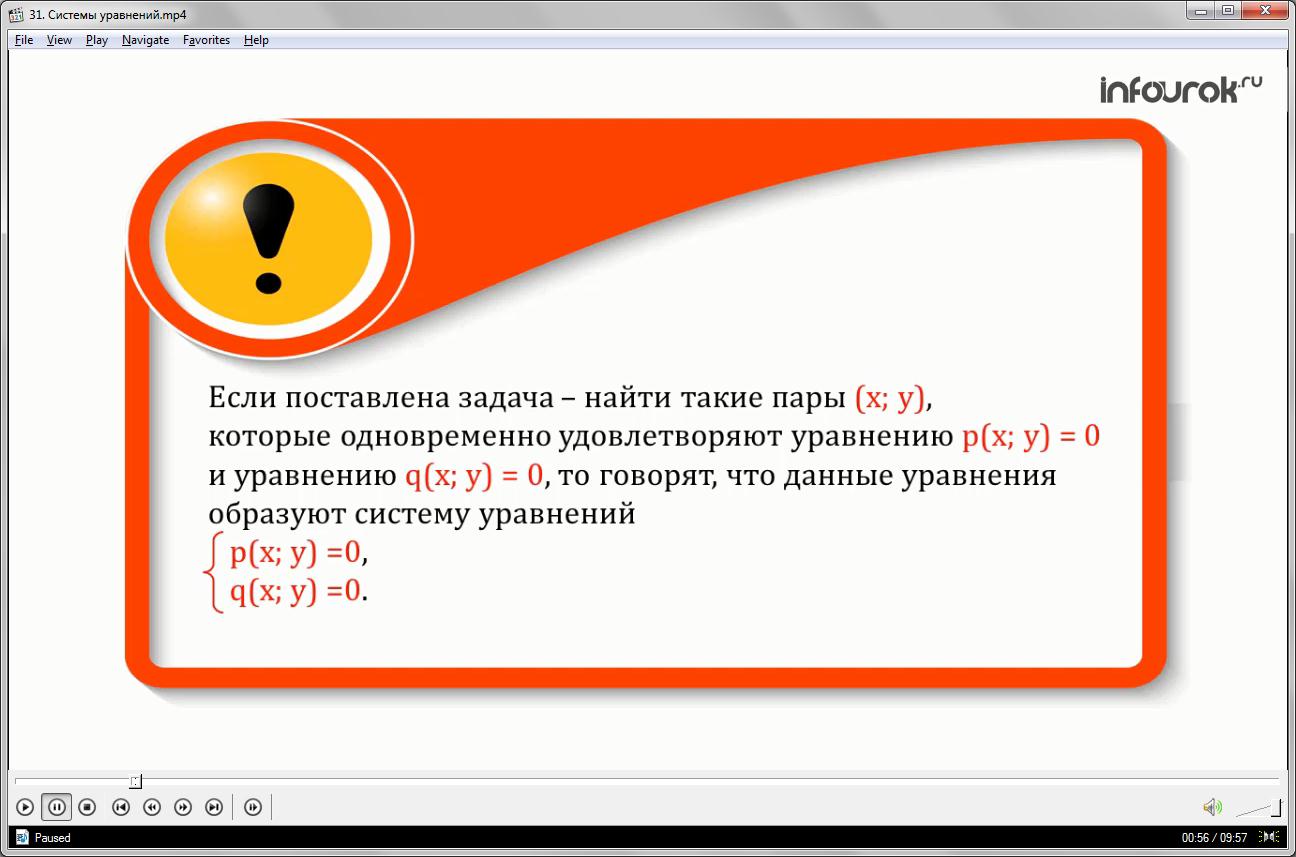
Определение первое. Если поставлена задача – найти такие пары икс и игрек, которые одновременно удовлетворяют уравнению пэ от икс игрек равно нулю и уравнению кю от икс игрек равно нулю, то говорят, что данные уравнения образуют систему уравнений :

пэ от икс игрек равно нулю

кю от икс игрек равно нулю

Определение второе.

Пару значенийикс и игрек, которая одновременно является решением и первого и второго уравнения системы, называют решением системы уравнений.

Определение третье.

Решить систему уравнений – значит найти все ее решения или установить, что решений нет.

По аналогии можно говорить и о системе трех уравнений с тремя неизвестными.

Пэ от икс игрек зэт равно нулю

Кю от икс игрек зэт равно нулю

эр от икс игрек зэт равно нулю

При этом надо найти тройки чисел икс игрек зэт, удовлетворяющие каждое уравнение системы. Вообще, можно говорить о системах с любым количеством уравнений и неизвестных.

Алгоритм решения системы уравнений прост: постепенный переход от сложного уравнения к более простому, но при этом выполнять равносильные преобразования.

Стремиться получить хотя бы одно линейное уравнение, а если происходит переход к уравнению-следствию, то обязательна проверка корней.

Определение четвертое.

Две системы уравнений называют равносильными, если они имеют одни и те же решения или решений не имеют.

Какие же способы решения систем уравнений являются равносильными?

Методы подстановки, алгебраического сложения, введения новых переменных приводят к равносильным преобразованиям

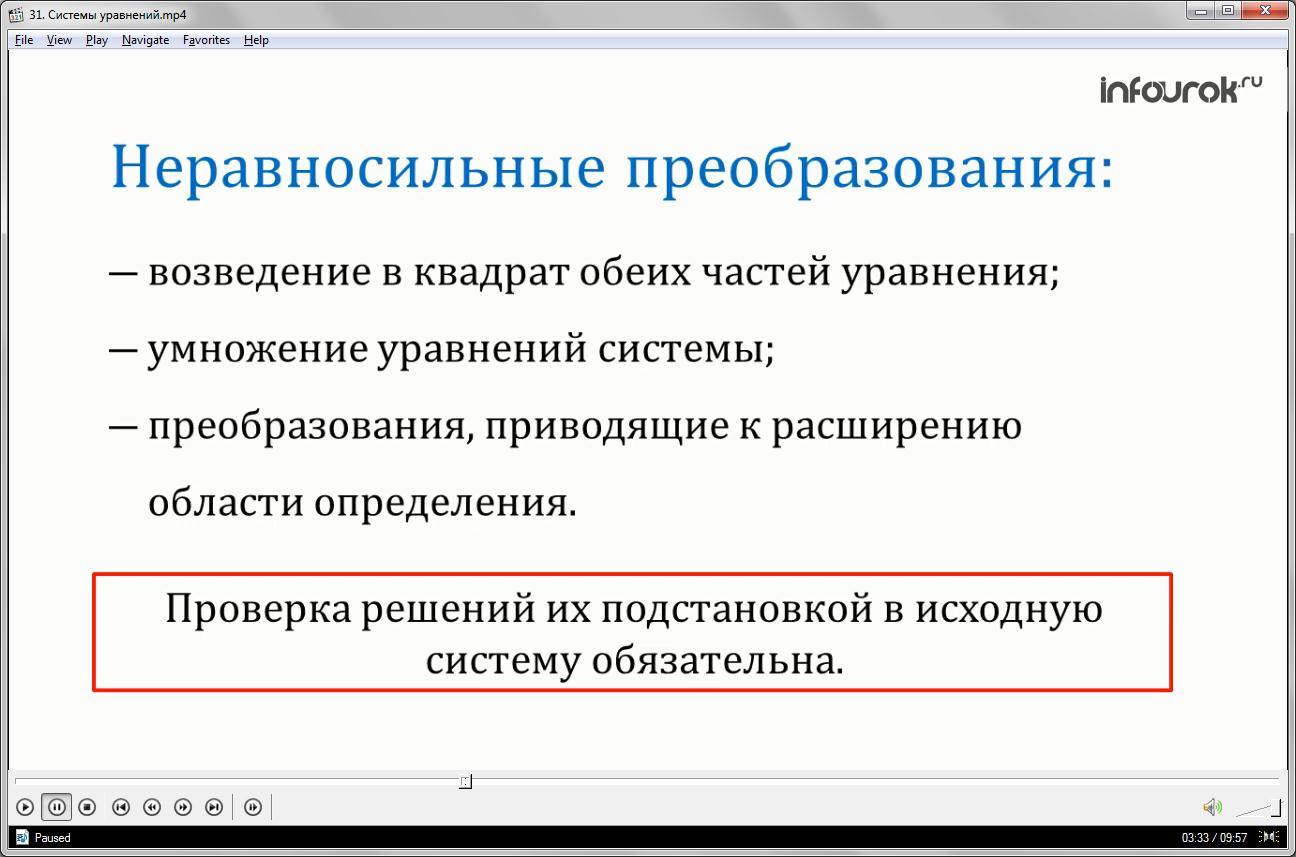
Если в процессе решения используются неравносильные преобразования хотя бы одного уравнения, к ним относятся возведение в квадрат обеих частей уравнения, умножение уравнений системы, преобразования, приводящие к расширению области определения, то необходима проверка решений их подстановкой в исходную систему.

Обратите внимание на рациональность решения системы.

Задание 1

Решить систему уравнений:

Первое уравнение — икс плюс игрек плюс два зэт равно четырем.

Второе уравнение – два икс плюс игрек плюс зэт равно единице.

Третье уравнение — икс плюс два игрек плюс зэт равно трем.

Решение

Можно заметить, что каждая переменная входит в систему четыре раза. Поэтому сложим все три уравнения (это равносильное преобразование) и получим: четыре икс плюс четыре игрек плюс четыре зэт равно восьми.

Разделим почленно обе части уравнения на четыре, получим: икс плюс игрек плюс зэт равно двум. В каждом уравнении системы будем выделять это равенство.

Тогда из второго уравнения системы имеем:

икс равен минус единице.

Из третьего уравнения получаем:

игрек равен единице.

Из первого уравнения имеем:

Итак, система уравнений имеет единственное решение — тройку чисел: минус один, один, два. Решение в проверке не нуждается, так как преобразования выполнялись равносильные.

Ответ: тройка чисел: минус один, один, два.

Задание 2

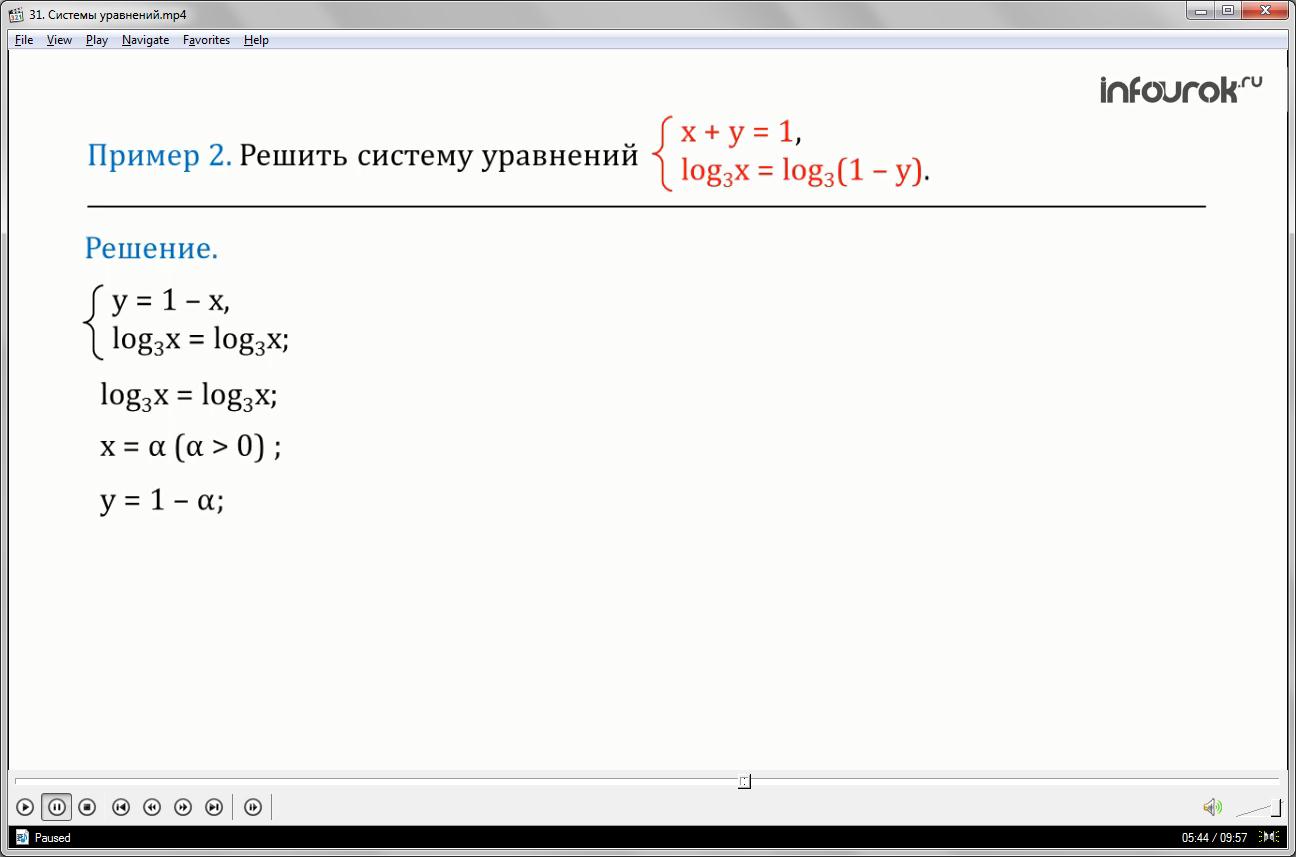
Решить систему уравнений

Первое уравнение – икс плюс игрек равно единице.

Второе уравнение логарифм икс по основанию три равно логарифму выражения один минус игрек по основанию три.

Решение

Выразим игрек через икс из первого уравнения системы и, подставляя его вместо игрека во второе уравнение, получаем уравнение: логарифм икс по основанию три равно логарифму икс по основанию три. Решениями этого уравнения являются все положительные числа. Каждому такому значению икс равное альфа, где альфа больше нуля, соответствует значение игрек равное один минус альфа. Следовательно, решениями исходной системы являются все пары чисел альфа и один минус альфа, где альфа — положительное число. Способ подстановки – равносильное преобразование.

Ответ: пара чисел: альфа и один минус альфа, где альфа — положительное число.

Задание 3

Решить систему уравнений: игрек квадрат плюс два икс игрек минус три икс квадрат равно нулю и игрек квадрат плюс три икс в квадрате равно четырем.

Решение

Можно заметить, что первое уравнение системы – однородное. Считая игрек неизвестной величиной, а икс – постоянной, решим его. Получим: игрек первое равно икс и игрек второе равно минус три икс.

Тем самым мы получили линейные уравнения. Исходная система сводится к совокупности двух систем уравнений:

первая система состоит из уравнений: игрек равен икс, игрек квадрат плюс три икс в квадрате равно четырем.

Вторая система состоит из уравнений: игрек равен минус три икс, игрек квадрат плюс три икс в квадрате равно четырем.

Решения первой системы — пара чисел: один и один и пара чисел: минус один, минус один. Вторую систему решаем способом подстановки.

Решениями системы является пара чисел: один, деленное на квадратный корень из трех и минус квадратный корень из трех, вторая пара: минус один, деленное на квадратный корень из трех и квадратный корень из трех.

При решении исходной системы все преобразования были равносильными, поэтому проверка не нужна.

Ответ: пара чисел: один и один; пара чисел: минус один, минус один; пара чисел: один, деленное на квадратный корень из трех, и минус квадратный корень из трех; пара: минус один, деленное на квадратный корень из трех, и квадратный корень из трех.

Задание 4

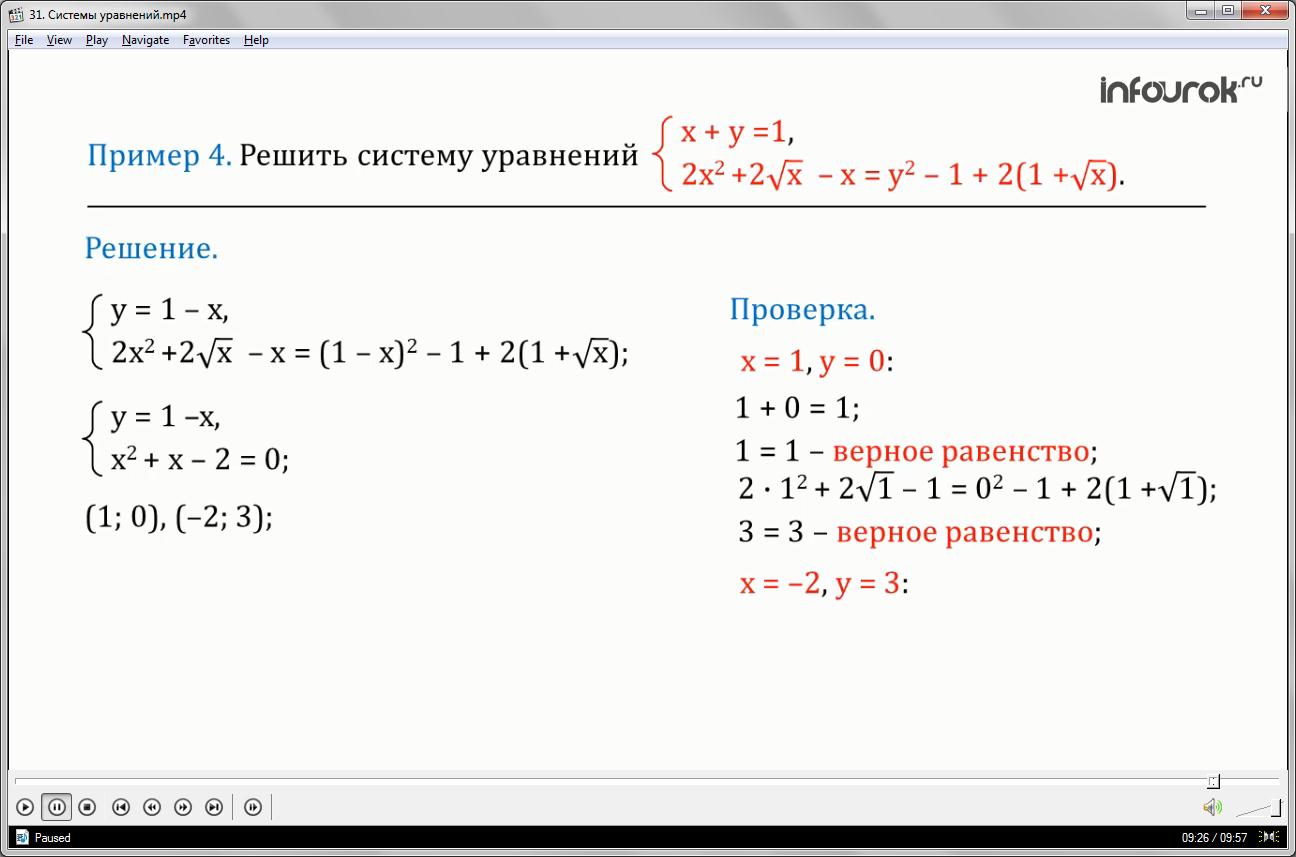
Решить систему уравнений

Первое уравнение – икс плюс игрек равно единице.

Второе — два икс в квадрате плюс два квадратных корней из икс минус икс равно игрек в квадрате минус один плюс два, умноженное на один плюс квадратный корень из икс.

Решение

Выразим игрек из первого уравнения и подставим во второе, перенесем во втором уравнении все члены в левую часть и, приведя подобные слагаемые, получим систему уравнений:

игрек равен один минус икс и икс в квадрате плюс икс минус два равно нулю.

Решением системы является пара чисел: один и ноль и пара чисел: минус два и три.

Эта система является следствием исходной, поэтому проверка обязательна.

Проверка

Проверим подстановкой в исходную систему уравнений, является ли каждая пара чисел решением данной системы.

Проверим первое уравнение.

Если икс равен единице, игрек равен нулю, то получаем верное равенство,

и во втором уравнении получаем

верное равенство. Значит, пара чисел: один и ноль — решение системы.

Проверяем вторую пару чисел: минус два и три. Если икс равен минус двум, игрек равен трем, то первое уравнение системы — верное равенство. А второе уравнение неверно, так как квадратный корень из минус двух не определён,

поэтому пара чисел: минус два и три не является решением системы.

Источник

Построение графиков функций

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

x	y
0	-1
1	2

x	y
0	2
1	1

x	y
0	0
1	2

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.