Как вывести формулу абсолютной погрешности

Как вывести формулу абсолютной погрешности

Погрешности прямых измерений. Промах. Систематическая погрешность. Случайная погрешность. Полная погрешность. Погрешности косвенных измерений. Запись результата измерений

Измерить физическую величину – это значит сравнить ее с однородной величиной, принятой за единицу меры.

Различают прямые и косвенные измерения.

Если измеряемая величина непосредственно сравнивается с мерой, то измерения называются прямыми. Например, измерения линейных размеров тел с помощью масштабной линейки и т.д.

Если измеряется не сама искомая величина, а некоторые другие величины, связанные с ней функциональной зависимостью, то измерения называются косвенными. Например, измерения объема, ускорения и т.д.

Из-за несовершенства средств и методик измерения, органов чувств при любом измерении неизбежны отклонения результатов измерений от истинных величин. Эти отклонения называются погрешностями измерений.

Погрешности измерений делятся на систематические, случайные и промахи.

1.1. Промахи, связанные с неправильными отсчетами по прибору, неправильными записями и т.д., приводят к очень большой по абсолютной величине погрешности. Они, как правило, не укладываются в общую закономерность измеренных величин. Обнаруженный промах следует отбросить.

1.2. Систематическими погрешностями Δx_сист называются погрешности, которые сохраняются при повторных измерениях одной и той же величины x или изменяются по определенному закону.

Систематические погрешности подразделяются на несколько групп. Отметим только приборную погрешность.

Систематическая приборная погрешность определяется по классу точности прибора, который указывается на приборе следующими цифрами: 0,01; 0,02; 0,05; 1,0; 2,5; 4,0. Класс точности показывает предельно допустимое значение систематической погрешности, выраженной в процентах от верхнего предела на выбранном диапазоне измерений. Например, предел измерения вольтметра с классом точности 0,5 равен 200 В. Систематическая погрешность равна 0,5% от 200В. Следовательно, систематическая погрешность вольтметра равна 1 В.

Если на приборе класс точности не указан, то погрешность равна половине цены наименьшего деления шкалы прибора.

1.3. Случайными называются погрешности, которые изменяются беспорядочно при повторных измерениях одной и той же физической величины при одинаковых условиях.

Оценим случайную погрешность. Пусть при измерении какой-либо физической величины было произведено N измерений и были получены значения x₁, x₂, … x_N. Тогда наиболее вероятным значением измеряемой величины является ее среднее арифметическое значение

Результаты измерений x₁, x₂, … x_N «рассеиваются» вокруг среднего. В качестве меры «рассеяния» результатов наблюдения вокруг среднего служит среднее квадратичное отклонение

Пусть a будет истинным, но неизвестным значением измеряемой величины x. Доказано, что вероятность попадания результатов измерения величины x в интервал значений от (a – S) до (a + S) оказывается равной α = 0,68.

Вероятность попадания результатов наблюдений в более широкие интервалы (a – 2S, a + 2S) и (a – 3S, a + 3S) равна α = 0,95 и α = 0,99 соответственно.

Вероятность попадания в заданный интервал значений величины x называется доверительной вероятностью, а сам интервал – доверительным интервалом.

Однако, таким образом полученный доверительный интервал справедлив при большом значении N. В учебных лабораториях, как правило, приходится ограничиваться небольшим числом измерений. В этом случае доверительный интервал находят с помощью коэффициента Стьюдента, который зависит от числа измерений N и доверительной вероятности α. В таблице 1 приведены коэффициенты Стьюдента для различного числа наблюдений при доверительных вероятностях α = 0,68; 0,95; 0,99.

Источник

Оценка погрешностей результатов измерений

Оценка погрешностей результатов измерений

Погрешности измерений и их типы

Любые измерения всегда производятся с какими-то погрешностями, связанными с ограниченной точностью измерительных приборов, неправильным выбором, и погрешностью метода измерений, физиологией экспериментатора, особенностями измеряемых объектов, изменением условий измерения и т. д. Поэтому в задачу измерения входит нахождение не только самой величины, но и погрешности измерения, т. е. интервала, в котором вероятнее всего находится истинное значение измеряемой величины. Например, при измерении отрезка времени t секундомером с ценой деления 0,2 с можно сказать, что истинное значение его находится в интервале от с до с. Таким образом, измеряемая величина всегда содержит в себе некоторую погрешность , где и X – соответственно истинное и измеренное значения исследуемой величины. Величина называется абсолютной погрешностью (ошибкой) измерения, а выражение , характеризующее точность измерения, называется относительной погрешностью.

Вполне естественно стремление экспериментатора произвести всякое измерение с наибольшей достижимой точностью, однако такой подход не всегда целесообразен. Чем точнее мы хотим измерить ту ил иную величину, тем сложнее приборы мы должны использовать, тем больше времени потребуют эти измерения. Поэтому точность окончательного результата должна соответствовать цели проводимого эксперимента. Теория погрешностей дает рекомендации, как следует вести измерения и как обрабатывать результаты, чтобы величина погрешности была минимальной.

Все возникающие при измерениях погрешности обычно разделяют на три типа – систематические, случайные и промахи, или грубые ошибки.

Систематические погрешности обусловлены ограниченной точностью изготовления приборов (приборные погрешности), недостатками выбранного метода измерений, неточностью расчетной формулы, неправильной установкой прибора и т. д. Таким образом, систематические погрешности вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Величина этой погрешности систематически повторяется либо изменяется по определенному закону. Некоторые систематические ошибки могут быть исключены (на практике этого всегда легко добиться) путем изменения метода измерений, введение поправок к показаниям приборов, учета постоянного влияния внешних факторов.

Хотя систематическая (приборная) погрешность при повторных измерениях дает отклонение измеряемой величины от истинного значения в одну сторону, мы никогда не знаем в какую именно. Поэтому приборная погрешность записывается с двойным знаком

Случайные погрешности вызываются большим числом случайных причин (изменением температуры, давления, сотрясения здания и т. д.), действия которых на каждое измерение различно и не может быть заранее учтено. Случайные погрешности происходят также из-за несовершенства органов чувств экспериментатора. К случайным погрешностям относятся и погрешности обусловленные свойствами измеряемого объекта.

Исключить случайны погрешности отдельных измерений невозможно, но можно уменьшить влияние этих погрешностей на окончательный результат путем проведения многократных измерений. Если случайная погрешность окажется значительно меньше приборной (систематической), то нет смысла дальше уменьшать величину случайной погрешности за счет увеличения числа измерений. Если же случайная погрешность больше приборной, то число измерений следует увеличить, чтобы уменьшить значение случайной погрешности и сделать ее меньше или одного порядка с погрешностью прибора.

2. Оценка систематической (приборной) погрешности

При прямых измерениях значение измеряемой величины отсчитывается непосредственно по шкале измерительного прибора. Ошибка в отсчете может достигать нескольких десятых долей деления шкалы. Обычно при таких измерениях величину систематической погрешности считают равной половине цены деления шкалы измерительного прибора. Например, при измерении штангенциркулем с ценой деления 0,05 мм величина приборной погрешности измерения принимают равной 0,025 мм.

Цифровые измерительные приборы дают значение измеряемых ими величин с погрешностью, равной значению одной единицы последнего разряда на шкале прибора. Так, если цифровой вольтметр показывает значение20,45 мВ, то абсолютная погрешность при измерении равна мВ.

Систематические погрешности возникают и при использовании постоянных величин, определяемых из таблиц. В подобных случаях погрешность принимается равной половине последнего значащего разряда. Например, если в таблице значение плотности стали дается величиной, равной 7,9∙103 кг/м3, то абсолютная погрешность в этом случае равна кг/м3.

Некоторые особенности в расчете приборных погрешностей электроизмерительных приборов будут рассмотрены ниже.

При определении систематической (приборной) погрешности косвенных измерений функциональной величины используется формула

, (1)

где — приборные ошибки прямых измерений величины , — частные производные функции по переменной .

В качестве примера, получим формулу для расчета систематической погрешности при измерении объема цилиндра. Формула вычисления объема цилиндра имеет вид

.

Частные производные по переменным d и h будут равны

, .

Таким образом, формула для определения абсолютной систематической погрешности при измерении объема цилиндра в соответствии с имеет следующий вид

,

где и приборные ошибки при измерении диаметра и высоты цилиндра

3. Оценка случайной погрешности.

Доверительный интервал и доверительная вероятность

Для подавляющего большинства простых измерений достаточно хорошо выполняется так называемый нормальный закон случайных погрешностей (закон Гаусса), выведенный из следующих эмпирических положений.

1) погрешности измерений могут принимать непрерывный ряд значений;

2) при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,

3) чем больше величина случайной погрешности, тем меньше вероятность ее появления.

График нормального закона распределения Гаусса представлен на рис.1. Уравнение кривой имеет вид

, (2)

где — функция распределения случайных ошибок (погрешностей), характеризующая вероятность появления ошибки , σ – средняя квадратичная ошибка.

Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.

Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического . Величина которой определяется по формуле

, (3)

где — результат i-го измерения; — среднее арифметическое полученных значений; n – число измерений.

Чем больше число измерений, тем меньше и тем больше оно приближается к σ. Если истинное значение измеряемой величины μ, ее среднее арифметическое значение, полученное в результате измерений , а случайная абсолютная погрешность , то результат измерений запишется в виде .

Интервал значений от до , в который попадает истинное значение измеряемой величины μ, называется доверительным интервалом. Поскольку является случайной величиной, то истинное значение попадает в доверительный интервал с вероятностью α, которая называется доверительной вероятностью, или надежностью измерений. Эта величина численно равна площади заштрихованной криволинейной трапеции. (см. рис.)

Все это справедливо для достаточно большого числа измерений, когда близка к σ. Для отыскания доверительного интервала и доверительной вероятности при небольшом числе измерений, с которым мы имеем дело в ходе выполнения лабораторных работ, используется распределение вероятностей Стьюдента. Это распределение вероятностей случайной величины , называемой коэффициентом Стьюдента, дает значение доверительного интервала в долях средней квадратичной ошибки среднего арифметического .

. (4)

Распределение вероятностей этой величины не зависит от σ2, а существенно зависит от числа опытов n. С увеличением числа опытов nраспределение Стьюдента стремится к распределению Гаусса.

Функция распределения табулирована (табл.1). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n, и столбца, соответствующего доверительной вероятности α

Источник

Приложение А. Погрешности вычислений

Абсолютная и относительная погрешности

Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.

Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:

(А.1)

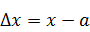
где а – приближенное значение числа х.

Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:

(А.2)

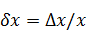
Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность . В дальнейшем значение принимается в качестве абсолютной погрешности приближенного числа а. Тогда истинное значение х находится в интервале .

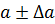
Источники погрешностей

Рассмотрим различные причины возникновения погрешностей.

Математическая модель задачи является неточной

Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).

Ошибки в исходных данных

Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.

Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.

Вычислительные ошибки (ошибки округления)

Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.

Вычислительные ошибки

Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно.

Представление чисел с плавающей точкой

Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от .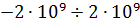

В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок:

(А.3)

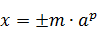
где m – мантисса, p – порядок, а – основание степени.

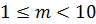
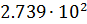
Например, число 273.9 можно представить в виде или в компьютерном представлении 2.739E+02.

В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности.

Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой

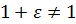
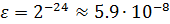
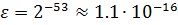
Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что . Например, для числа с одинарной точностью 1 + 0.00000001 = 1. Для одинарной точности , а для двойной точности .

Погрешность округления

При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность принимается равной половине единицы последнего разряда числа. Например, значение могло быть получено округлением чисел 0.73441, 0.73353 и др. При этом . При простом отбрасывании лишних разрядов эта погрешность увеличивается вдвое.

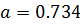
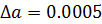
Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например:

Погрешность арифметических действий над приближенными числами

При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются:

, (А.4)

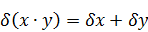
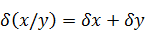
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:

(А.5)

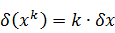
При сложении или вычитании чисел их абсолютные погрешности складываются:

(А.6)

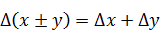
Относительная погрешность суммы положительных слагаемых вычисляется как:

. (А.7)

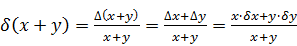
Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:

. (А.8)

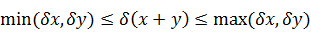
На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность .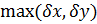

При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению:

1234 + 0.005678 = 1234.00005678

или в компьютерном представлении:

1.234Е+03 + 5.678Е-03 = 1.234005678Е+03

После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении.

Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях 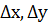результат их сложения в знаменателе может быть очень малым. Чтобы уменьшить погрешность при вычитании, необходимо строить вычислительные алгоритмы таким образом, чтобы избегать вычитания близких чисел.

Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.

Источник