Как вывести функцию суммарного спроса
Кривые рыночного спроса и предложения



Как получить функцию суммарного спроса?
Нередко у нас в наличие есть несколько функций спроса на определенное благо, отражающих желания и возможности отдельных индивидов или групп потребителей, а нам требуется описать суммарный спрос этих потребителей одной функцией. Другими словами определить рыночный спрос при всех возможных значениях цен на данное благо.
Функцию рыночного спроса на благо можно получить путем суммирования индивидуальных объемов спроса потребителей на рынке при различных ценах. Графически это будет выглядеть, как горизонтальное суммирование по оси Q всех индивидуальных величин спроса.
ЧИСЛОВОЙ ПРИМЕР. (КРИВАЯ СУММАРНОГО СПРОСА)
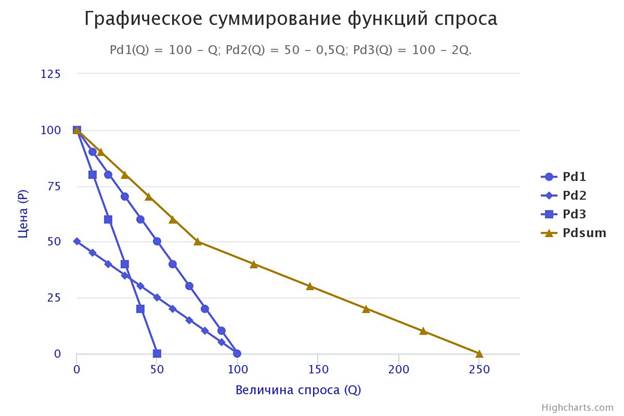
Величина спроса (Q)Цена (P)Графическое суммирование функций спроса
Графическое построение функции суммарного спроса (Pdsum(Q)) очень простое. Мы должны просуммировать величины спроса всех трех потребителей при различных ценах (P) в диапазоне от 0 до ∞. В соответствии с имеющимися у нас данными, отмечаем, что при ценах выше 100 ни один потребитель не будет предъявлять положительную величину спроса. При ценах в диапазоне от 50 до 100 только два потребителя готовы потреблять ненулевое количество блага. Суммируем эти количества и отмечаем их точками на графике. При ценах в диапазоне от 0 до 50 все три потребителя готовы предъявить ненулевой спрос на рассматриваемое благо. Зафиксируем суммарные значения величин спроса и также отметим их на графике. В итоге мы получили график кусочной функции с точками перегиба при P = 50 и 100, так как при этих ценах на рынок выйдут новые потребители.
Так как на графике мы получили линейную функцию спроса с точкой перегиба, то, чтобы описать ее функционально, нам потребуется записать систему, состоящую из трех условий:
7.5 Рыночная кривая спроса. Сложение индивидуальных кривых спроса
Мы определили, что количество потребителей положительно влияет на рыночный спрос. При увеличении количества потребителей на рынке спрос при каждом уровне цены растет. В соответствии с этим утверждением и производится сложение отдельных индивидуальных кривых спроса для получения общей рыночной кривой спроса: при каждом возможном уровне цены необходимо сложить величины индивидуальных спросов отдельных потребителей. Этот принцип называется «правило сложения по горизонтали». Данное правило существует для того, чтобы подчеркнуть, что сложению подвергаются именно величины индивидуальных спросов. Данное правило гласит, что складывать индивидуальные кривые спроса следует вправо, то есть по оси Q. Именно поэтому суммарная кривая рыночного спроса по сравнению с индивидуальными кривыми имеет более пологий вид: она как бы «растягивается» по оси Q. Сложение кривых спроса следует выполнять, начиная с максимально возможного значения цены блага, постепенно переходя к минимальной, то есть нулевой. Это обусловлено тем, что цена спроса – это максимальная цена, которую потребитель готов заплатить за товар.
Пример горизонтального сложения спроса
Для того, чтобы найти уравнение общего спроса, необходимо воспользоваться алгоритмом «сложения индивидуальных спросов на интервалах». Поясним на примере, что это такое.
В примере выше нам даны две прямых индивидуального спроса
Требуется определить уравнение общего спроса.
Вначале найдем интервалы цены для каждого спроса
Данные значения цен разбивают ось цены на следующие интервалы:
Рассмотрим отдельно каждый интервал цены
P ∈ [0;25] в этом интервале существуют оба спроса, поэтому Qобщий = Q1 + Q2
P ∈ [25;50] в этом интервале существует только Q1, поэтому Qобщий = Q1
P > 50 в этом интервале не существует ни одного спроса, поэтому Qобщий = 0
Рассмотрим частные случаи сложения функций спроса:
Один из спросов является горизонтальной линией
Если один из спросов является горизонтальной линией, это означает, что данный покупатель готов купить любой объем товара при данной цене. Другой покупатель имеет обычную убывающую линию спроса. Что будет суммарным спросом в этом случае?
Другими словами, что увидит продавец, который придет на данный рынок? При построении общего спроса не будем забывать, что линия спроса показывает максимальные цены, которые готов заплатить покупатель за разные объемы блага. Таким образом, при построении общего спроса мы должны выбрать максимальные уровни цены. Еще можно запомнить такое правило: горизонтальная линия спроса «стирает» все спросы, которые находятся под ней пи построении общего спроса.
Если один из спросов является вертикальной линией, то график суммарного спроса будет выглядеть так:
В этом случае один из потребителей готов купить определенный объем товара по какой-угодно цене (может быть, данный товар ему очень необходим). При сложении мы получаем, что график другого покупателя (с обычным убывающим спросом) двигается параллельно вправо.
ИНФОРМАЦИЯ О СВОБОДНЫХ МЕСТАХ
В настоящий момент активно набираю учеников на предстоящий учебный сезон. Есть около 10 мест
ТЕОРИЯ И ЗАДАНИЯ
ИНТЕРВЬЮ С УЧЕНИКАМИ
Интервью с Дмитрием Сорокиным, абсолютным победителем Всероссийской олимпиады по экономике 2009 года
Спрос и предложение
Задача №1. Определение изменения дохода при увеличении проданной продукции на одну единицу
Фирма имеет кривую спроса:
Задача №2. Коэффициент точечной эластичности
Для стимулирования сбыта своей продукции фирма «IBS» объявила о временном снижении цен на одну из моделей компьютера с 1000 до 800 долл. В результате за следующий месяц фирма продала в два раза больше компьютеров, чем обычно.
а) Как изменилась выручка фирмы?
б) Рассчитайте коэффициент точечной эластичности (по формуле, используемой в определении) и сделайте вывод о характере спроса на данную модель компьютера.
Задача №3. Эластичность спроса по цене
Функция задана уравнением
а) Выведите формулу эластичности этого спроса.
б) При какой цене эластичность спроса по цене составит – 0,5?
в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?
Задача №4. Функция суммарного спроса
а) Определить функцию суммарного спроса на основании данных об индивидуальном спросе:
Задача №5. Функция суммарного спроса
Известны данные об индивидуальном спросе:
а) Выведите уравнение кривой спроса аналитически.
б) Получите формулу эластичности по абсолютной величине в зависимости от цены.
Определите кривую суммарного спроса на основании данных об индивидуальном спросе: Q1 = 50 — 5P, где P
| 🎓 Заказ №: 22506 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Экономика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 249 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
Готовые задачи по экономике которые сегодня купили:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Информация
Материал предоставлен для ознакомительных целей и использование материала этого учебного пособия без указания автора учебника и ссылки на этот электронный ресурс недопустимо.
 Содержание
Содержание
5.3. От индивидуального спроса к рыночному спросу
Мы вывели кривую индивидуального спроса и объяснили с помощью эффектов дохода и замещения её отрицательный наклон. Но в большинстве исследований используется кривая рыночного спроса.
Покажем сначала, как можно сложить кривые индивидуального спроса геометрически. Затем рассмотрим алгебраическое решение задачи.
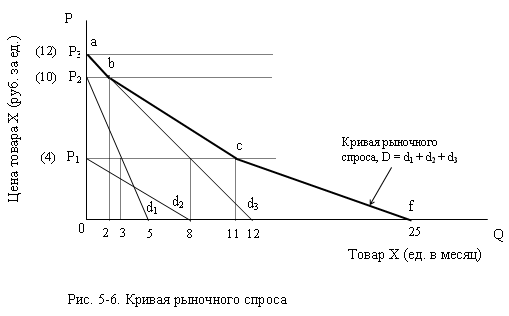
Поскольку все функции индивидуального спроса линейны, постольку сложение их даёт тоже линейную функцию рыночного спроса. Но полученная линия будет ломаной, состоящей из нескольких отрезков, каждый из которых соответствует определённому диапазону изменения цены. Найдём критические точки, соединив которые мы получим эту ломаную кривую.
При рыночной цене Р3 величина спроса на рынке равна 0, так как ни один из потребителей не готов покупать по этой цене даже единицу товара Х (D = d1+d2+d3 = 0+0+0 = 0). Мы получили первую точку на кривой рыночного спроса, а с координатами (0,Р3).
В диапазоне цены между Р3 и Р2 единственным покупателем товара является 3-й потребитель. Рыночный спрос при цене Р2 равен: D = d1+d2+d3 = 0+0+2 = 3. Координаты второй точки кривой рыночного спроса, b – (2,P2). Поэтому в этом ценовом диапазоне рыночная кривая спроса совпадает с d3 на участке ab.
Наконец, при Р=0 все три потребителя предъявят спрос: D = d1+d2+d3 = 5+8+12=25. Соединив прямой линией точку f (25,0) с точкой с, получим последний участок кривой рыночного спроса сf.
Как получить уравнение функции рыночного спроса, если известны уравнения функций индивидуального спроса?
Изображённые на рис. 5-6 функции индивидуального спроса, описываются уравнениями:
Для того, чтобы определить какой будет величина совокупного спроса при любом уровне цены на рынке, нужно алгебраически сложить уравнения индивидуального спроса: Q d рын. = Q1 + Q2 + Q3.
Однако простое решение: Q d рын = 25 – 3,5Р, было бы ошибочным, поскольку оно не учитывает того, что в некоторых ценовых диапазонах рыночный спрос состоит из спроса не всех, а только отдельных потребителей. Поэтому при суммировании приходится эти диапазоны учитывать. Определим их.
Из уравнения (3) найдем, что при Р ≥ 12 спрос 3-го потребителя будет равен нулю (на рис. 5-6 Р3 =12). Из уравнения (2) следует, что если Р≥ 10, то спрос 2-го потребителя равен 0 ( на рис. 5-6 этому уровню цены соответствует Р2. Из уравнения (1) находим, что при Р≥ 4 спрос 1-го потребителя тоже равен 0.
Следовательно, если 10 ≤ Р ≤ 12, то рыночный спрос состоит только из спроса 3-го потребителя. В этом ценовом диапазоне уравнение функции рыночного спроса представлено только уравнением (3): Q d рын = Q3 = 12 – P.
В диапазоне 4 ≤ Р ≤ 10 спрос на рынке предъявляют 3-й и 1-й потребители. Поэтому на этом участке рыночный спрос: Q d рын. = Q1 + Q3 = (5 – 0,5Р) + (12 – Р) = 17 – 1,5Р.
Наконец, если 0 ≤ Р ≤ 4, то Q d рын. = Q1 + Q2 + Q3 = (5 – 0,5Р) + (8 – 2Р) + (12 – Р) = 25 –3,5Р.
Понятно, что кривая рыночного спроса, являясь горизонтальной суммой нисходящих индивидуальных кривых спроса, также имеет отрицательный наклон. Даже, если некоторые потребители имеют восходящую кривую спроса, то они не делают погоды на данном рынке, так как подавляющее большинство покупателей имеют нормальные, нисходящие кривые спроса. Это ещё одна причина, по которой мы можем не беспокоиться о товаре Гиффена в дальнейшем анализе.
Есть несколько интересных случаев, когда рыночный спрос формируется не как простая сумма спроса отдельных покупателей. Эти случаи – так называемый «эффект повального увлечения» (bandwagon effect), «эффект сноба» и «эффект Веблена».



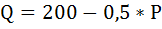
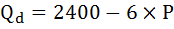

 Содержание
Содержание