Как вывести график в матлабе
Как вывести график в матлабе
1. Построение двумерных графиков функций
В результате вычислений в системе MATLAB обычно получается большой массив данных, который трудно анализировать без наглядной визуализации. Поэтому система визуализации, встроенная в MATLAB, придаёт этому пакету особую практическую ценность.
Графические возможности системы MATLAB являются мощными и разнообразными. В первую очередь целесообразно изучить наиболее простые в использовании возможности. Их часто называют высокоуровневой графикой. Это название отражает тот приятный факт, что пользователю нет никакой необходимости вникать во все тонкие и глубоко спрятанные детали работы с графикой.
Например, нет ничего проще, чем построить график функции одной вещественной переменной. Следующие команды
x = 0 : 0.01 : 2;
y = sin( x );
вычисляют массив y значений функции sin для заданного набора аргументов.
После этого одной единственной командой
удаётся построить вполне качественно выглядящий график функции:
MATLAB показывает графические объекты в специальных графических окнах, имеющих в заголовке слово Figure (изображение, внешний вид, фигура).
При построении графиков функций сразу проявляется тот факт, что очень большую часть работы MATLAB берёт на себя. Мы в командной строке ввели лишь одну команду, а система сама создала графическое окно, построила оси координат, вычислила диапазоны изменения переменных x и y; проставила на осях метки и соответствующие им числовые значения, провела через опорные точки график функции некоторым, выбранным по умолчанию, цветом; в заголовке графического окна надписала номер графика в текущем сеансе работы.
Если мы, не убирая с экрана дисплея первое графическое окно, вводим и исполняем ещё один набор команд
x = 0 : 0.01 : 2;
z = cos( x );
Если нужно второй график провести «поверх первого графика», то перед исполнением второй графической команды plot, нужно выполнить команду
hold on
которая предназначена для удержания текущего графического окна. В результате будет получено следующее изображение:
Того же самого можно добиться, потребовав от функции plot построить сразу несколько графиков в рамках одних и тех же осей координат:
x = 0 : 0.01 : 2;
y = sin( x ); z = cos( x );
У такого способа есть ещё одно (кроме экономии на команде hold on) преимущество, так как разные графики автоматически строятся разным цветом.
К недостаткам указанных способов построения нескольких графиков в пределах одних и тех же осей координат относится использование одного и того же диапазона изменения координат, что при несопоставимым значениях двух функций приведёт к плохому изображению графика одной из них.
Если всё же нужно одновременно визуализировать несколько графиков так, чтобы они не мешали друг другу, то это можно сделать двумя способами. Во-первых, можно построить их в разных графических окнах. Например, построив графики функций sin и cos в пределах одного графического окна (показано выше), вычисляем значения для функции exp:
w = exp( x );
После этого выполняем команды
которые построят график функции exp в новом графическом окне, так как команда figure создаёт новое (добавочное) графическое окно, и все последующие за ней команды построения графиков выводят их в новое окно:
Вторым решением рассматриваемой задачи показа сразу нескольких графиков без конфликта диапазонов осей координат является использование функции subplot. Эта функция позволяет разбить область вывода графической информации на несколько подобластей, в каждую из которых можно вывести графики различных функций.
subplot(1,2,1); plot(x,y,x,z)
subplot(1,2,2); plot(x,w)
в результате чего получаем графическое окно следующего вида:
Диапазоны изменения переменных на осях координат этих подобластей независимы друг от друга.
Если для одиночного графика диапазоны изменения переменных вдоль одной или обоих осей координат слишком велики, то можно воспользоваться функциями построения графиков в логарифмических масштабах. Для этого предназначены функции semilogx, semilogy и loglog. Подробную информацию по использованию этих функций всегда можно получитьпри помощи команды
help имя_функции
набираемой с клавиатуры и выполняемой в командном окне системы MATLAB.
Итак, уже рассмотренные примеры показывают, как подсистема высокоуровневой графики MATLABа легко справляется с различными случаями построения графиков, не требуя слишком большой работы от пользователя. Ещё одним таким примером является построение графиков в полярных координатах. Например, если нужно построить график функции r = sin( 3 f ) в полярных координатах, то следующие несколько команд
phi = 0 : 0.01 : 2*pi; r = sin( 3* phi );
Как вывести график в матлабе
Обычная графика MATLAB
Построение графиков точками и отрезками прямых
Графики в логарифмическоми полулогарифмическом масштабе
Гистограммы и диаграммы
Графики специальных типов
Создание массивов данных для трехмерной графики
Построение графиков трехмерных поверхностей, сечений и контуров
Средства управления подсветкой и обзором фигур
Средства оформления графиков
Одновременный вывод нескольких графиков
Управление цветовой палитрой
Окраска трехмерных поверхностей
Двумерные и трехмерные графические объекты
Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса (GUI). Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов.
Описанию графических функций и команд посвящена обширная электронная книга в формате PDF. Объем материала по графике настолько велик, что помимо вводного описания графики в уроке 3 в этой книге даются еще два урока по средствам обычной и специальной графики. Они намеренно предшествуют систематизированному описанию большинства функций системы MATLAB, поскольку графическая визуализация вычислений довольно широко используется в последующих материалах книги. При этом графические средства системы доступны как в командном режиме вычислений, так и в программах. Этот урок рекомендуется изучать выборочно или выделить на него не менее 4 часов.
Построение графиков отрезками прямых
Функции одной переменной у(х) находят широкое применение в практике математических и других расчетов, а также в технике компьютерного математического моделирования. Для отображения таких функций используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси — горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки функции у(х). Эти точки соединяются друг с другом отрезками прямых, т. е. при построении графика осуществляется линейная интерполяция для промежуточных точек. Поскольку MATLAB — матричная система, совокупность точек у(х) задается векторами X и Y одинакового размера.
Команда plot служит для построения графиков функций в декартовой системе координат. Эта команда имеет ряд параметров, рассматриваемых ниже.
plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.
Приведенный ниже пример иллюстрирует построение графиков двух функций — sin(x) и cos(x), значения функции которых содержатся в матрице Y, а значения аргумента х хранятся в векторе X:
На рис. 6.1 показан график функций из этого примера. В данном случае отчетливо видно, что график состоит из отрезков, и если вам нужно, чтобы отображаемая функция имела вид гладкой кривой, необходимо увеличить количество узловых точек. Расположение их может быть произвольным.
Рис. 6.1. Графики двух функций в декартовой системе координат
plot(Y) — строит график у(г), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot (real (Y). imag(Y)). Во всех других случаях мнимая часть данных игнорируется.
Вот пример использования команды plot(Y):
Соответствующий график показан на рис. 6.2.
Рис. 6.2. График функции, представляющей вектор Y с комплексными элементами
plot(X.Y.S) — аналогична команде plot(X.Y), но тип линии графика можно задавать с помощью строковой константы S.
Значениями константы S могут быть следующие символы.
Глава 3. Работа с графиками в MatLab
MatLab предоставляет богатый инструментарий по визуализации данных. Используя внутренний язык, можно выводить двумерные и трехмерные графики в декартовых и полярных координатах, выполнять отображение изображений с разной глубиной цвета и разными цветовыми картами, создавать простую анимацию результатов моделирования в процессе вычислений и многое другое.
Функция plot
Рассмотрение возможностей MatLab по визуализации данных начнем с двумерных графиков, которые обычно строятся с помощью функции plot(). Множество вариантов работы данной функции лучше всего рассмотреть на конкретных примерах.
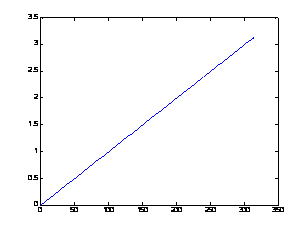
Предположим, что требуется вывести график функции синуса в диапазоне от 0 до 
В результате получится вектор столбец со множеством значений от 0 до 
и выведем результат на экран
В результате получим график, представленный на рис. 3.1.
Представленная запись функции plot() показывает, что сначала записывается аргумент со множеством точек оси Ох, а затем, аргумент со множеством точек оси Oy. Зная эти значения, функция plot() имеет возможность построить точки на плоскости и линейно их интерполировать для придания непрерывного вида графика.
Рис. 3.1. Отображение функции синуса с помощью функции plot().
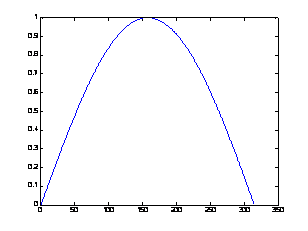
Функцию plot() можно записать и с одним аргументом x или y:
в результате получим два разных графика, представленные на рис. 3.2.
Анализ рис. 3.2 показывает, что в случае одного аргумента функция plot() отображает множество точек по оси Oy, а по оси Оx происходит автоматическая генерация множества точек с единичным шагом. Следовательно, для простой визуализации вектора в виде двумерного графика достаточно воспользоваться функцией plot() с одним аргументом.
Для построения нескольких графиков в одних и тех же координатных осях, функция plot() записывается следующим образом:
x = 0:0.01:pi;
y1 = sin(x);
y2 = cos(x);
plot(x,y1,x,y2);
Результат работы данного фрагмента программы представлен на рис. 3.3.
Рис. 3.2. Результаты работы функции plot() с одним аргументом:
Рис. 3.3. Отображение двух графиков в одних координатных осях.
Аналогичным образом можно построить два графика, используя один аргумент функции plot(). Предположим, что есть два вектора значений
которые требуется отобразить на экране. Для этого объединим их в двумерную матрицу
в которой столбцы составлены из векторов y1 и y2 соответственно. Такая матрица будет отображена функцией
plot([y1’ y2’]); % апострофы переводят вектор-строку
% в вектор-столбец
в виде двух графиков (рис. 3.4).
Рис. 3.4. Отображение двумерной матрицы в виде двух графиков.
Два вектора в одних осях можно отобразить только в том случае, если их размерности совпадают. Когда же выполняется работа с векторами разных размерностей, то они либо должны быть приведены друг к другу по числу элементов, либо отображены на разных графиках. Отобразить графики в разных координатных осях можно несколькими способами. В самом простом случае можно создать два графических окна и в них отобразить нужные графики. Это делается следующим образом:
x1 = 0:0.01:2*pi;
y1 = sin(x1);
x2 = 0:0.01:pi;
y2 = cos(x2);
plot(x1, y1); % рисование первого графика
figure; % создание 2-го графического окна
plot(x2, y2); % рисование 2-го графика во 2-м окне
Функция figure, используемая в данной программе, создает новое графическое окно и делает его активным. Функция plot(), вызываемая сразу после функции figure, отобразит график в текущем активном графическом окне. В результате на экране будут показаны два окна с двумя графиками.
Неудобство работы приведенного фрагмента программы заключается в том, что повторный вызов функции figure отобразит на экране еще одно новое окно и если программа будет выполнена дважды, то на экране окажется три графических окна, но только в двух из них будут актуальные данные. В этом случае было бы лучше построить программу так, чтобы на экране всегда отображалось два окна с нужными графиками. Этого можно достичь, если при вызове функции figure в качестве аргумента указывать номер графического окна, которое необходимо создать или сделать активным, если оно уже создано. Таким образом, вышеприведенную программу можно записать так.
x1 = 0:0.01:2*pi;
y1 = sin(x1);
x2 = 0:0.01:pi;
y2 = cos(x2);
figure(1); %создание окна с номером 1
plot(x1, y1); % рисование первого графика
figure(2); % создание графического окна с номером 2
plot(x2, y2); % рисование 2-го графика во 2-м окне
При выполнении данной программы на экране всегда будут отображены только два графических окна с номерами 1 и 2, и в них показаны графики функций синуса и косинуса соответственно.
В некоторых случаях большего удобства представления информации можно достичь, отображая два графика в одном графическом окне. Это достигается путем использования функции subplot(), имеющая следующий синтаксис:
Рассмотрим пример отображения двух графиков друг под другом вышеприведенных функций синуса и косинуса.
x1 = 0:0.01:2*pi;
y1 = sin(x1);
x2 = 0:0.01:pi;
y2 = cos(x2);
figure(1);
subplot(2,1,1); % делим окно на 2 строки и один столбец
plot(x1,y1); % отображение первого графика
subplot(2,1,2); % строим 2-ю координатную ось
plot(x2,y2); % отображаем 2-й график в новых осях
Результат работы программы показан на рис. 3.5.
Аналогичным образом можно выводить два и более графиков в столбец, в виде таблицы и т.п. Кроме того, можно указывать точные координаты расположения графика в графическом окне. Для этого используется параметр position в функции subplot():
subplot(‘position’, [left bottom width height]);
где left – смещение от левой стороны окна; bottom – смещение от нижней стороны окна; width, height – ширина и высота графика в окне. Все эти переменные изменяются в пределах от 0 до 1.
Рис. 3.5. Пример работы функции subplot.
Ниже представлен фрагмент программы отображения графика функции синуса в центре графического окна. Результат работы показан на рис. 3.6.
x1 = 0:0.01:2*pi;
y1 = sin(x1);
subplot(‘position’, [0.33 0.33 0.33 0.33]);
plot(x1,y1);
В данном примере функция subplot() смещает график на треть от левой и нижней границ окна и рисует график с шириной и высотой в треть графического окна. В результате, получается эффект рисования функции синуса по центру основного окна.
Таким образом, используя параметр position можно произвольно размещать графические элементы в плоскости окна.
Рис. 3.6. Пример работы функции subplot с параметром position.
Оформление графиков
Пакет MatLab позволяет отображать графики с разным цветом и типом линий, показывать или скрывать сетку на графике, выполнять подпись осей и графика в целом, создавать легенду и многое другое. В данном параграфе рассмотрим наиболее важные функции, позволяющие делать такие оформления на примере двумерных графиков.
Функция plot() позволяет менять цвет и тип отображаемой линии. Для этого, используются дополнительные параметры, которые записываются следующим образом:
Обратите внимание, что третий параметр записывается в апострофах и имеет обозначения, приведенные в таблицах 3.1-3.3. Маркеры, указанные ниже записываются подряд друг за другом, например,
‘ko’ – на графике отображает черными кружками точки графика,
‘ko-‘ – рисует график черной линией и проставляет точки в виде кружков.
Табл. 3.1. Обозначение цвета линии графика
| Маркер | Цвет линии |
| c | голубой |
| m | фиолетовый |
| y | желтый |
| r | красный |
| g | зеленый |
| b | синий |
| w | белый |
| k | черный |
Табл. 3.2. Обозначение типа линии графика
| Маркер | Цвет линии |
| — | непрерывная |
| — | штриховая |
| : | пунктирная |
| -. | штрих-пунктирная |
Табл. 3.3. Обозначение типа точек графика
| Маркер | Цвет линии |
| . | точка |
| + | плюс |
| * | звездочка |
| o | кружок |
| x | крестик |
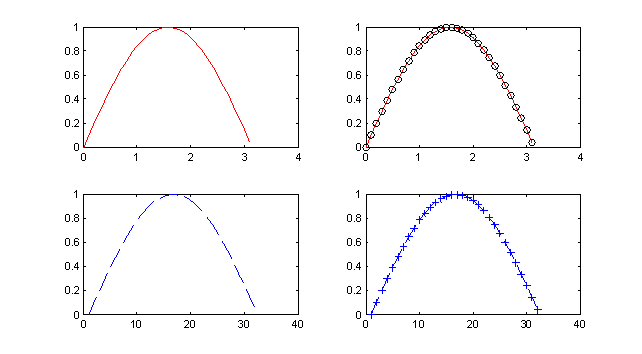
Ниже показаны примеры записи функции plot() с разным набором маркеров.
subplot(2,2,1); plot(x,y,’r-‘);
subplot(2,2,2); plot(x,y,’r-‘,x,y,’ko’);
subplot(2,2,3); plot(y,’b—‘);
subplot(2,2,4); plot(y,’b—+’);
Результат работы фрагмента программы приведен на рис. 3.7. Представленный пример показывает, каким образом можно комбинировать маркеры для достижения требуемого результата. А на рис. 3.7 наглядно видно к каким визуальным эффектам приводят разные маркеры, используемые в программе. Следует особо отметить, что в четвертой строчке программы по сути отображаются два графика: первый рисуется красным цветом и непрерывной линией, а второй черными кружками заданных точек графика. Остальные варианты записи маркеров очевидны.
Рис. 3.7. Примеры отображения графиков с разными типами маркеров
Из примеров рис. 3.7 видно, что масштаб графиков по оси Ox несколько больше реальных значений. Дело в том, что система MatLab автоматически масштабирует систему координат для полного представления данных. Однако такая автоматическая настройка не всегда может удовлетворять интересам пользователя. Иногда требуется выделить отдельный фрагмент графика и только его показать целиком. Для этого используется функция axis() языка MatLab, которая имеет следующий синтаксис:
axis( [ xmin, xmax, ymin, ymax ] ),
где название указанных параметров говорят сами за себя.
Воспользуемся данной функцией для отображения графика функции синуса в пределах от 0 до 
subplot(1,2,2);
plot(x,y);
axis([0 pi 0 1]);
Из результата работы программы (рис. 3.8) видно, что несмотря на то, что функция синуса задана в диапазоне от 0 до 

Рис. 3.8. Пример работы функции axis()
В заключении данного параграфа рассмотрим возможности создания подписей графиков, осей и отображения сетки на графике. Для этого используются функции языка MatLab, перечисленные в табл. 3.4.
Таблица 3.4. Функции оформления графиков
| Название | Описание |
| grid [on, off] | Включает/выключает сетку на графике |
| title(‘заголовок графика’) | Создает надпись заголовка графика |
| xlabel(‘подпись оси Ox’) | Создает подпись оси Ox |
| ylabel(‘подпись оси Oy’) | Создает подпись оси Oy |
| text(x,y,’текст’) | Создает текстовую надпись в координатах (x,y). |
Рассмотрим работу данных функций в следующем примере:
Из результата работы данной программы, представленного на рис. 3.9, видно каким образом работают функции создания подписей на графике, а также отображение сетки графика.
Таким образом, используя описанный набор функций и параметров, можно достичь желаемого способа оформления графиков в системе MatLab.
Рис. 3.9. Пример работы функций оформления графика
2. Графика matlab
График даёт самую полную общую информацию о функции, поэтому в системах компьютерной математики большое внимание уделяется средствам построения графиков функций.
Функция plot() строит графики кривых с массивами значений абсцисс 

Строка s используется для задания параметров графика: типа, толщины и цвета рисуемой линии, а также формы и размера меток на графике. Строка s может отсутствовать, тогда MATLAB устанавливает параметры, действующие по умолчанию: все кривые выводятся сплошными линиями, окрашенными циклически в шесть различных цветов.
Переменная s представляет собой строку символов, и эту строку можно подготовить в отдельной команде или записать непосредственно в команде построения графика, например
Таблица кодировки типов линий при выводе графика функции
Таблица кодировки цвета линии графика функции
Таблица кодировки меток на графике
^ v > > x=0:0.01:3; y=exp(x).*sin(9*x); plot(x, y,’r-‘)
Для построения графиков используется специальный графический редактор, который строит на экране графическое окно и в нём рисует график. Вызывается графический редактор автоматически при выполнении графических функций. По умолчанию производится разметка осей координат и иногда выводится заголовок сверху графика. Графический редактор имеет свои средства модификации графика и нанесения на график различных надписей и символов. Например, заголовок создаёт функция titke(‘text’), причём в качестве параметра text можно использовать и формулу.
Пример. Построить график функции 
Текст можно вывести в заданное координатами 

>> text(0.5, 15, ‘grafik y=exp(x)sin(9x)’)
Координаты вывода текста можно указать на графике мышью, если использовать функцию 
нужно указать мышью место на графике и щёлкнуть.
На одном чертеже можно построить графики нескольких функций, для этого нужно попарно перечислить векторы, задающие абсциссы и ординаты. Для идентификации графиков можно использовать команду legend(), позволяющую связать с каждой кривой некоторую текстовую информацию.
Пример. Построить на одном чертеже графики функций 

Имеется другой способ размещения на одном чертеже графиков нескольких функций: сформировать матрицу, столбцы которой должны содержать нужные ординаты. Ординаты обычно удобно задавать строками, тогда для построения графиков строки необходимо транспонировать.
Пример. Построить на одном чертеже графики функций 
а) Построить график функции 


6) Построить график функции 


в) Построить на одном чертеже графики функций 
г) Построить на одном чертеже графики функций 

д) Построить на одном чертеже графики функций 

Функция ezplot() применяется для рисования графиков неявно заданных функции двух переменных и параметрически заданных функций. Эта функция рисует также графики функций одной переменной, причём, в огтличие от функции plot(), шаг и нужные массивы значений абсцисс и ординат соэдаются автоматически. Функция ezplot() автоматически выводит над графиками наименование функций.
Пример. Построить на промежутке 








В первой команде используется функция hold, чтобы сохранить рисунок для последующего наложения на него второго рисунка.
Пример. Найти начальное приближение решения системы
Рисунок показывает, что система имеет четыре решения, приближённые значения которых есть 



2.3. Построение нескольких рисунков в одном графическом окне
В одном графическом окне можно разместить несколько рисунков, используя функцию subplot(N,M,K). Эта функция создаёт массив графиков, состоящий из N рисунков по вертикали и M рисунков по горизонтали. В результате выполнения функции subplot(N,M,K) активным становится рисунок с номером K. Нумерация ведётся слева направо и сверху вниз. Крайний слева рисунок из верхнего ряда считается первым, а крайний справа из нижнего ряда имеет номер N*M.
Пример. В одном графическом окне построить графики четырёх функций: 







Решение. Выполним следующие команды, не закрывая графического окна:
>> subplot(2,2,1), ezplot(‘x^2’,[-5,5]), xlabel(»),grid
>> subplot(2,2,2), ezplot(‘exp(x)’,[-2,2]), xlabel(»),grid
>> subplot(2,2,3), ezplot(‘log(x)’,[0,5]), xlabel(»),grid
>> subplot(2,2,4), ezplot(‘sqrt(x)’,[0,10]), xlabel(»),grid
В командах вывода графиков использована функция xlabel(‘’) с аргументом в виде пустой строки, которая отменяет вывод обозначения горизонтальной оси. Если этого не сделать, то символ обозначения оси наложится на наименование функций нижних графиков.
Функция fplot(‘f(x)’, [xmin, xmax]), аналогично функции plot(), строит график функции f(x), однако при использовании функции fplot() не требуется задавать массив значений аргумента и вычислять массив
значений функции, всё это делается автоматически. 
Пример. Построить график функции 

Решение. Используем функцию fplot():
2.5. Трёхмерная графика
Чтобы построить поверхность 

Пример. Построить поверхность 
>> x=0:0.2:8; y=0:0.2:4; [X, Y]=meshgrid(x, y); Z=2*cos(X+Y)+Y.*cos(X-Y); mesh(X, Y,Z)
Функция mesh() строит расцвеченную сетчатую поверхность, используя различную окраску вершин и рёбер.
Кроме функции mesh(), для изображения поверхности имеются и другие функции:
meshc()−строится сетчатая поверхность с линиями уровня;
meshz()−строится сетчатая поверхность и отсчётная плоскость;
surf()−строится расцвеченная поверхность;
surfc()−строится расцвеченная поверхность с линиями уровня;
surfl()−строится расцвеченная поверхность с подсветкой;
waterfall−строится поверхность без прорисовки ребер.
Пример. Построим поверхность 
После построения рисунков для каждого рисунка можно выполнить масштабирование функцией axis([-Inf Inf —Inf Inf —Inf Inf]). Например, второй рисунок промасштабирует команда
При масштабировании определяются действительные интервалы изменения величин по всем координатам и рисунки становятся выразительнее.
1) Построить поверхность 

2) Эту же поверхность 
3) Эту же поверхность 
4) Построить поверхность 

5) Выбрать сетку и построить поверхность 
6) Построить в одном графическом окне три поверхности 
7) Выбрать сетку и построить в одном графическом окне четыре поверхности 


8) Построить в одном окне поверхность 


9) Построить поверхность